- #1
Ujjwal Basumatary
- 17
- 0
Homework Statement
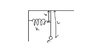
A pendulum of mass ##m## and length ##L## is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. What is the angular frequency of the bob?
Homework Equations
Angular frequency for angular simple harmonic motion is given by $$\omega=\sqrt{\frac{\alpha}{\theta}}=\sqrt{\frac{K}{I}}$$
Where
##\theta=## Displaced angle
##\alpha=## Angular acceleration
##I=## Moment of inertia
##K=## Equivalent force constant
The Attempt at a Solution
I have done the problem in the following way:
Consider a small angular displacement of ##\theta##. The torque about the the hinge at any instant is then given by $$\Gamma = -mgL\sin\theta-kxh$$ where ##x## is the displacement of the spring. But ##x=h\sin\theta## and therefore our equation becomes $$\Gamma = -mgL\sin\theta -mh^2\sin\theta$$
But ##\sin\theta \approx \theta## for small ##theta##. Therefore the torque is given by $$\Gamma = I\alpha=-mgL\theta -mh^2\theta$$ Thus we have ##\Gamma \propto -\theta##, which is the condition for angular SHM. Recalling that ##I=mL^2## we finally obtain $$\omega=\sqrt{\frac{\alpha}{\theta}} = \sqrt{\frac{K}{I}} = \sqrt{\frac{kh^2+mgL}{mL^2}}$$
Please look and tell me if there's anything wrong with the solution. Thank you.