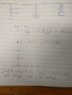- #1
spsch
- 111
- 21
- Homework Statement
- A hanging spring (k=100) is in equilibrium (without the mass M). It is then pulled down to 50 cm from equilibrium. Now a mass of 3 kg is attached and the spring released.
a) what is the speed of the mass after it has moved up 10 cm?
b) what are the heights at which the mass has a speed of 0.8 m/s?
- Relevant Equations
- ma = -kx
E = mgx + 1/2kx^2 + 1/2mv^2
Dear all,
I am back with another Spring problem.
I have tried to use the insights I gained from your help last time:
https://www.physicsforums.com/threa...nded-from-a-spring.972942/page-3#post-6190934
I figured I start with calculating the new equilibrium by ## x =\frac{-mg}{k} ##
And then subtracting that from the 50 cm to get the amplitude which gave me -20.6 cm.
I then set up the energy equation with a fixed coordinate system as I learned in the above thread:
With the -20.6 being A.
## E = \frac {1}{2}*m*v^2+\frac {1}{2}*k*x^2+mgx ##
so
## \frac {1}{2}*k*A^2+mgA = \frac {1}{2}*m*v^2+\frac {1}{2}*k*x^2+mgx ##
My solution and calculation are in the pictures attached.
For b) I could only think of using the quadratic formula, is there a better way?
Is my work correct?
Thank you all
I am back with another Spring problem.
I have tried to use the insights I gained from your help last time:
https://www.physicsforums.com/threa...nded-from-a-spring.972942/page-3#post-6190934
I figured I start with calculating the new equilibrium by ## x =\frac{-mg}{k} ##
And then subtracting that from the 50 cm to get the amplitude which gave me -20.6 cm.
I then set up the energy equation with a fixed coordinate system as I learned in the above thread:
With the -20.6 being A.
## E = \frac {1}{2}*m*v^2+\frac {1}{2}*k*x^2+mgx ##
so
## \frac {1}{2}*k*A^2+mgA = \frac {1}{2}*m*v^2+\frac {1}{2}*k*x^2+mgx ##
My solution and calculation are in the pictures attached.
For b) I could only think of using the quadratic formula, is there a better way?
Is my work correct?
Thank you all