Spring/pendulum problem

[MusNothus]

Homework Statement

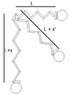
You have a pendulum with a ball of mass m at the end, and the pendulum is held parallel to the ground. This pendulum is also a spring, however, with spring constant k and equilibrium length L. You let go of the weight. What is L', the new length of the spring at the bottom of the swing, and what is the velocity of the ball?

Homework Equations

Conservation of mechanical energy E=(1/2)m*v^2 + m*g*h + (1/2)k*x^2
(where k is the spring constant)
Integral of force with respect to time = change in momentum
Work equations
other conservation laws that I may not be thinking of

The Attempt at a Solution

I've tried creating equations for the force and integrating it, but if I do it in terms of the angle of the pendulum, I have to make that a function of time and I haven't been able to figure out how much time it would take to reach the bottom of the swing. I've also tried conservation of mechanical energy, but I end up not knowing both the KE or the spring force so I can't get anywhere. I haven't taken a math class in two years, but I've had linear algebra, multi-variable calc, and differential equations so you can explain the solution in terms of those if you like. I guess I'm just a bit rusty because I can't get this one.

 

[MusNothus]

Oh, and I know this isn't all that advanced, but I thought that this was the category where I should post this.

 

[gabbagabbahey]

Since the spring will be extending as the pendulum swings downward, both its radial and tangential components will change; and you will end up solving two ODEs. You will need to solve the radial ODE in order to determine L'.

Once you know L', then you can use CoE to determine the velocity. I recommend setting the problem up such that the height of the mass at its lowest point is defined as zero, so that the final gravitational potential energy is zero and the initial GPE is mgL'. You will have to resolve the Forces that act on the mass into both tangential and radial components (or, alternatively x and y components).

Why don't you show us what you get for your differential equations for each component?

 

[borgwal]

I don't think the question is meant to be that difficult that you would have to solve ODEs. You already have one equation involving both L' and v (conservation of energy: except you should not have both an h and an x in there: you can relate h to x and L). The second equation you'd get by assuming that at the bottom of the swing, the ball is momentarily in a circular orbit: more precisely, once you know the curvature of the orbit, you know what the centripetal acceleration is. Since at the bottom of the swing you also know the forces on the ball, you get a second equation involving only L' and v.

 

[MusNothus]

Do you mean I can just use the equation for centripetal acceleration = v^2 / R, where R would be the length of the spring at the bottom?

I thought about doing this before, but wasn't sure if I could use that equation in this situation. I figured that maybe I could since at the bottom of the swing (assuming that the bottom is where the spring is most stretched, which might not be true if the spring constant is high enough) the outward radial force is equal to the inward radial force and the velocity is perpendicular to radial force. But yeah, if I can do that, then this is really easy, and I was totally over thinking it.

 

[borgwal]

Yes, that's what I meant. All you need for this to apply is that the velocity be horizontal at the bottom, which it is by definition of "bottom of swing."

 

[MusNothus]

Alright, thanks a lot for the help.

 

[TobyC]

You can't assume that the velocity will be horizontal at the bottom of the swing...? What are you basing that assumption on?

I interpret the phrase 'bottom of the swing' to mean directly below the pivot, which doesn't as far as I can see have to necessarily be the same as the lowest point reached by the mass.

 

[MusNothus]

Yeah, when the mass is at its lowest point, the velocity will be horizontal (obviously, because that's when the y component of its velocity vector is zero because it has stopped moving down and is about to start moving up), but it won't be horizontal at the point directly below the pivot unless that is also the lowest point it reaches (and it's not). I figured out that you really do have to do it as differential equations and it's easiest to do those in polar coordinates and just solve for the angle at which the radial velocity is zero.

 

[cupid.callin]

- use mechanical energy conservation to find the speed of ball at lowermost point.

- use the speed in the eqn of centripetal force ... (spring force) - (gravity) = centripital force. find spring force.

- simply use it to find L'

 

[TobyC]

- use mechanical energy conservation to find the speed of ball at lowermost point.

But you need to know the length of the spring at the lowest point in order to do that right? Or do you mean find the speed in terms of the length? You also don't know what angle the spring makes with the vertical at its lowest point, so that is another unknown.

- use the speed in the eqn of centripetal force ... (spring force) - (gravity) = centripital force. find spring force.

But its acceleration is not going to be completely directed towards the pivot when it is at its lowest point, so I don't think that will work, you'd need to take the component of gravity acting along the spring which you'd need to know the angle for.

Also, even then it would be wrong, because the length of the spring is not constant, so its acceleration is not just centripetal acceleration.

 

[cupid.callin]

But you need to know the length of the spring at the lowest point in order to do that right? Or do you mean find the speed in terms of the length? You also don't know what angle the spring makes with the vertical at its lowest point, so that is another unknown.

Angle?
Spring will itself be vertical when at lowest point ... so angle will be 0 !

And how i did it was to use x as extension when spring is vertical (ball at lowest point)

But i got a really annoying answer so I'm missing something. :(

But its acceleration is not going to be completely directed towards the pivot when it is at its lowest point, so I don't think that will work, you'd need to take the component of gravity acting along the spring which you'd need to know the angle for.

Also, even then it would be wrong, because the length of the spring is not constant, so its acceleration is not just centripetal acceleration.

Please draw a diagram of what you mean by lowest point ... and what force has a horizontal component at lowest point?

 

[TobyC]

Angle?
Spring will itself be vertical when at lowest point ... so angle will be 0 !

And how i did it was to use x as extension when spring is vertical (ball at lowest point)

But i got a really annoying answer so I'm missing something. :(

Please draw a diagram of what you mean by lowest point ... and what force has a horizontal component at lowest point?

The question here is quite ambiguous. There are two possible meanings, it could be asking for the length of the spring when it is directly below the pivot point, or it could be asking for the length of the spring when the mass is at its lowest point. These will not necessarily be the same because the lowest point occurs when the velocity is horizontal but there is no reason for the velocity to be horizontal when the spring is vertical because the spring's length can change.

However you interpret the question though I don't think your method works, because your centripetal acceleration method only applies when the motion is a circle, which isn't the case here. If you try to apply it here there will be too many unknowns.

I think the post a couple of posts up is right about having to do it through writing down the equations of motion and trying to solve them. I had a quick go at that yesterday but I ended up with a very complicated one that I couldn't solve, so I still don't know what the answer is. That's probably down to my lack of experience of solving complicated differential equations.

 

[TobyC]

Yeah, when the mass is at its lowest point, the velocity will be horizontal (obviously, because that's when the y component of its velocity vector is zero because it has stopped moving down and is about to start moving up), but it won't be horizontal at the point directly below the pivot unless that is also the lowest point it reaches (and it's not). I figured out that you really do have to do it as differential equations and it's easiest to do those in polar coordinates and just solve for the angle at which the radial velocity is zero.

But at the lowest point the radial velocity won't necessarily be zero? The vertical velocity will be zero, but since the mass is going to be at an angle when it is at its lowest point, the vertical velocity is going to be made up of components from the radial AND the tangential velocity.

 

[cupid.callin]

Do you see in figure that ball is at lowest point when spring is vertical.
You are going too deep in question ...

and IMO the spring will be vertical when ball will have only horizontal speed.

However you interpret the question though I don't think your method works, because your centripetal acceleration method only applies when the motion is a circle, which isn't the case here. If you try to apply it here there will be too many unknowns.

centripetal acceleration is not just about circular motion ... even elliptical and helical motions have centripetal acceleration. what makes some motion with non circular is that either their centripetal acceleration is not constant or they also have some tangential acceleration ... and still you can use centripetal acceleration at some point of your motion .. provided that the length from center and tangential velocity is known.

 

[TobyC]

Do you see in figure that ball is at lowest point when spring is vertical.
You are going too deep in question ...

and IMO the spring will be vertical when ball will have only horizontal speed.

Drawing a picture of what you think doesn't make it right. You could be right, there might be a physical argument I've overlooked which means that the velocity has to be horizontal when the spring is vertical, but I'm not going to believe that until you give me the argument.

Your intuition is obviously telling you that the velocity will be horizontal, but my intuition tells me it won't be. Take an extreme example and imagine doing this experiment with a very heavy mass and a very weak spring, if I picture that in my head it seems like the mass should just plummet downwards very quickly and reach its lowest point before the spring has a chance to become vertical, when it is vertical the mass will be on its way back up having already reached its lowest point.

Alternatively, imagine a very long pendulum so that its natural period is far longer than the natural period of the spring. If you set that going with with small amplitude oscillations you are going to have the spring going up and down many times within each pendulum swing, so there's no reason for the lowest point to occur when the spring is vertical.

centripetal acceleration is not just about circular motion ... even elliptical and helical motions have centripetal acceleration. what makes some motion with non circular is that either their centripetal acceleration is not constant or they also have some tangential acceleration ... and still you can use centripetal acceleration at some point of your motion .. provided that the length from center and tangential velocity is known.

I'm aware that centripetal acceleration arises whenever you describe something with polar coordinates. However, if the motion is not circular then there will be more to the radial acceleration than just the centripetal acceleration. You can't set the radial acceleration equal to the centripetal acceleration as you tried to do in your original post by writing the incorrect equation:

spring force - weight = centripetal force.