- #1
- 716
- 162
I understand the whole explanation about why static friction does no work-- I'm just confused about one of the consequences of that.
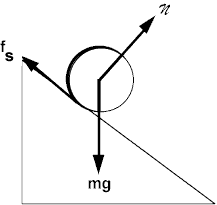
Consider the picture above. The ring is being pulled down the incline with a force of mg*sin(θ). If you analyze the system about the axis at the center of mass of the ring, the only force that can provide a torque to the ring is the force of static friction (all other forces are applied at the center of mass). The ring will rotate about that axis if it is rolling without slipping, at a rate of ω=v/r which will increase as the velocity of the center of mass (v) is accelerating. Since the angular speed changes with time, there is a net torque on the ring that has to be provided by the force of static friction. If a torque is applied, and there is an angular displacement (which must happen for the ring to be rotating) there is work done W=∫τdθ. Therefore, it seems as though the force of static friction must be doing work.
Consider the picture above. The ring is being pulled down the incline with a force of mg*sin(θ). If you analyze the system about the axis at the center of mass of the ring, the only force that can provide a torque to the ring is the force of static friction (all other forces are applied at the center of mass). The ring will rotate about that axis if it is rolling without slipping, at a rate of ω=v/r which will increase as the velocity of the center of mass (v) is accelerating. Since the angular speed changes with time, there is a net torque on the ring that has to be provided by the force of static friction. If a torque is applied, and there is an angular displacement (which must happen for the ring to be rotating) there is work done W=∫τdθ. Therefore, it seems as though the force of static friction must be doing work.