- #1
jonjacson
- 447
- 38
Statics, compute force in member of a frame [SOLVED]
Hi guys, I opened this thread but then I saw the mistake and I tried to delete it but I don´t know how, I´m sorry.
I´ll show the problem using a picture:
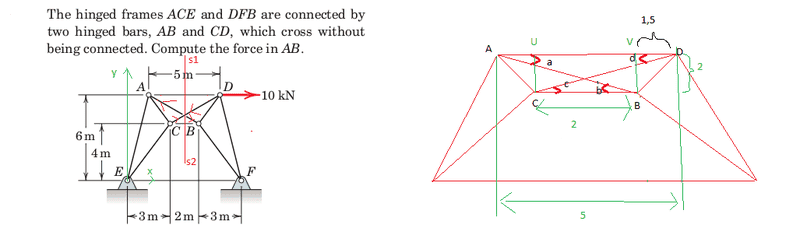
Sum forces = 0
Sum moments = 0
M = r x f
Well my idea is using the method of sections, I´ll cut the bars AB and CD at the middle point and I´ll have two systems the one AEC and the bars AB, CD until their middle points and the system BDF and the bars AB, CD until their middle points too.
Once I have those two systems I can apply the moment equation around E and F, since there are only two external unknown forces to those systems, and they are the forces AB, CD for both systems and the 10 kn for the BDF system, I´ll have two equations and two unkowns, where I´ll be able to get AB.
The problem is that I get an answer of 5,2 KN for AB and the book says the result is 3,78KN.
So I´ll show the calculations that maybe are wrong.
I´d like to comment the fact that there are two black lines between CB and AD but I think they are not bars, since they are not connected to the points A,B,C,D I´m assuming those lines are there to show the meaning of the distances between those points. If I´m wrong all my calculations won´t correspond to the problem and obviously that´s the reason I´m getting a wrong result.
I think that the four angles a,b,c,d that I show on the right image are the same.
To calculate the angle d for example, I´ll use triangle DUC on the right image. Since the distance AD is 5, and the structure is symmetric there must be the same distance between AU and VD, but we know that from C to B there are 2 meters so the distance VD= AU = 3/2= 1,5 meters.
Once I know that, getting the angle is easy, using the triangle DUC for example:
angle d= arctg(2/2+1.5)= 29.74 º
Now let´s calculate the moments around point E:
In this case the external forces acting at A and C are shown with red arrows, assuming that AB is a compression force and CD is a tension force, at this point I´m not sure about that but I know that they should be opposite since if they were both tension or compression forces system ACE should rotate around E.
Me= Rec x CD + Rea x AB= (3,4) x (CD cosθ, CD sinθ) + (1.5, 6) x (-AB cosθ, AB sinθ)=
3 CD sinθ - 4 CD cosθ +1.5 AB sinθ + 6 AB cosθ = 0 ; equation 1
Now I calculate the moment around point F for the system on the right of the vertical red line:
Mf= Rfb x -AB + Rfd x 10kn + Rfd x -CD = (-3,4) x (AB cosθ, -AB sinθ ) + (-1.5, 6) x (10,0) + (-1.5, 6) x (- CD cosθ, -CD cosθ ) = 3 AB sinθ - 4 AB cos θ -60 + 1.5 CD sinθ +6 CD cos θ = 0;
equation 2
Now I use the value of the angle θ=29,74 and I get from equation 1:
AB (5.2 + 0.74) + CD (1.49 - 3.47) = 0 --------> CD = AB 2.25 ; MISTAKE WAS HERE
Equation 2 looks like this:
-60 + CD(0.74 + 5.2) + AB ( 1,49 - 3,47)= 0;
I substitute the value of CD at the second equation:
-60 + 5.94 ( 3 AB) -1,98 AB = 0;
Finally:
AB = 60/15.84 = 3.78 KN ;
Well I don´t know if I calculated incorrectly the angles, or if I simply made a mathematical mistake.
Hopefully you will see it, the correct result is 3,78 KN Compression.
edit:
I found the mistake CD = 3 AB not 2,25. But I don´t know how to delete the thread since it is clear now and I woulnd´t like to make you lose your time reading this.
ANybody knows if it´s possible to delete the thread? I can´t find a tool to do that.
Thanks
Hi guys, I opened this thread but then I saw the mistake and I tried to delete it but I don´t know how, I´m sorry.
Homework Statement
I´ll show the problem using a picture:
Homework Equations
Sum forces = 0
Sum moments = 0
M = r x f
The Attempt at a Solution
Well my idea is using the method of sections, I´ll cut the bars AB and CD at the middle point and I´ll have two systems the one AEC and the bars AB, CD until their middle points and the system BDF and the bars AB, CD until their middle points too.
Once I have those two systems I can apply the moment equation around E and F, since there are only two external unknown forces to those systems, and they are the forces AB, CD for both systems and the 10 kn for the BDF system, I´ll have two equations and two unkowns, where I´ll be able to get AB.
The problem is that I get an answer of 5,2 KN for AB and the book says the result is 3,78KN.
So I´ll show the calculations that maybe are wrong.
I´d like to comment the fact that there are two black lines between CB and AD but I think they are not bars, since they are not connected to the points A,B,C,D I´m assuming those lines are there to show the meaning of the distances between those points. If I´m wrong all my calculations won´t correspond to the problem and obviously that´s the reason I´m getting a wrong result.
I think that the four angles a,b,c,d that I show on the right image are the same.
To calculate the angle d for example, I´ll use triangle DUC on the right image. Since the distance AD is 5, and the structure is symmetric there must be the same distance between AU and VD, but we know that from C to B there are 2 meters so the distance VD= AU = 3/2= 1,5 meters.
Once I know that, getting the angle is easy, using the triangle DUC for example:
angle d= arctg(2/2+1.5)= 29.74 º
Now let´s calculate the moments around point E:
In this case the external forces acting at A and C are shown with red arrows, assuming that AB is a compression force and CD is a tension force, at this point I´m not sure about that but I know that they should be opposite since if they were both tension or compression forces system ACE should rotate around E.
Me= Rec x CD + Rea x AB= (3,4) x (CD cosθ, CD sinθ) + (1.5, 6) x (-AB cosθ, AB sinθ)=
3 CD sinθ - 4 CD cosθ +1.5 AB sinθ + 6 AB cosθ = 0 ; equation 1
Now I calculate the moment around point F for the system on the right of the vertical red line:
Mf= Rfb x -AB + Rfd x 10kn + Rfd x -CD = (-3,4) x (AB cosθ, -AB sinθ ) + (-1.5, 6) x (10,0) + (-1.5, 6) x (- CD cosθ, -CD cosθ ) = 3 AB sinθ - 4 AB cos θ -60 + 1.5 CD sinθ +6 CD cos θ = 0;
equation 2
Now I use the value of the angle θ=29,74 and I get from equation 1:
AB (5.2 + 0.74) + CD (1.49 - 3.47) = 0 --------> CD = AB 2.25 ; MISTAKE WAS HERE
Equation 2 looks like this:
-60 + CD(0.74 + 5.2) + AB ( 1,49 - 3,47)= 0;
I substitute the value of CD at the second equation:
-60 + 5.94 ( 3 AB) -1,98 AB = 0;
Finally:
AB = 60/15.84 = 3.78 KN ;
Well I don´t know if I calculated incorrectly the angles, or if I simply made a mathematical mistake.
Hopefully you will see it, the correct result is 3,78 KN Compression.
edit:
I found the mistake CD = 3 AB not 2,25. But I don´t know how to delete the thread since it is clear now and I woulnd´t like to make you lose your time reading this.
ANybody knows if it´s possible to delete the thread? I can´t find a tool to do that.
Thanks
Last edited: