Statics Maximum Weight Problem

[CharlesL]

A big HI to everyone in the forum. I am new to this awesome forum. Perfect for my engineering studies! :)

Anyway, here's my problem.
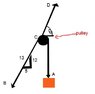
The cords BCA and CD can each support a maximum load of 500N. Determine the maximum weight of the crate(A) that can be hoisted at a constant velocity, and the angle 0 for equilibrium.

What I've done:
Using the equations of equilibrium,
$$\sum$$Fx=0
DC cos (angle) = CB sin 22.6
500N cos (angle) = 500 sin 22.6
angle = 67.4

$$\sum$$Fy=0
DC sin (angle) - CB cos 22.6 = A
500 sin 67.4 = A + 500 cos 22.6
A = 0.1N (a value which does not seems right to me)

 

[elbarto]

From what I could tell of your diagram, it looks like BCA is all 1 piece that wraps around the pully and CD is another piece that connects to the middle of the pully. If that is the case, then in you solution you assume that if the load in BC is 500, then the load in CD is 500.

If you think about it, if BC is 500 then AC must also be 500. you are getting 0.1 because if the BC==CD=500, then both of the cables will make the same angle to the X axis therefore cancleing out each other. [Remember there is nothing in the question suggesting that because the cables can each handle 500, that they infact carry this load]

The way I solved the problem is:

1) let the weight A=1, this will give u force in AC (and obviously BC) of 1
2)sum forces in the X and Y. both will have the 2 unkowns in them, Fcd and theata
3)divide one equation by the other (you will need to think about this) cancle out Fcd.
4)once you have theata, you can then solve for Fcd
5)you will now know the 3 tension forces, Fac Fbc Fcd, and which ever force is the highest will indicate the member that is critical
6)you know the maximum load for any member is 500, so use this to scale the load "A" so that the force in the critical member is 500

I got theata=78.7, A=255

This is the method I think you would find most usefull. you can also do it the way you started by allowing BC=500, but this will give you a load of 980 in member CD, which is higher then 500 so you would end up having to scale anyway. I usually start at the applied loads/reactions and work from there.

Hope this helps, I have given you a rough idea on my approach to the probelm (not saying it is the right or only way), so have a go at solving it using the steps above and see how you go.

Elbarto

 

[CharlesL]

Elbarto, thank you for clearing that up for me. The method you showed me is simpler and clearer than what I've seen. Anyway there's just one more thing, when i get Fcd as 1.96N and i have to scale it to A , so i'll have put it in a ratio wise like Fcd : A ? Since I am going to use this method in my coming exam.

Once again, I thank you for taking your time to explain everything to me.

Charles

 

[elbarto]

Elbarto, thank you for clearing that up for me. The method you showed me is simpler and clearer than what I've seen. Anyway there's just one more thing, when i get Fcd as 1.96N and i have to scale it to A , so i'll have put it in a ratio wise like Fcd : A ? Since I am going to use this method in my coming exam.

Once again, I thank you for taking your time to explain everything to me.

Charles

Basically if you have found Fcd to be 1.96 (which is exactly what I got), then for every 1 unit you apply at A, you will expect

Fac to increase by 1 unit.
Fbc to increase by 1 unit.
Fcd to increase by 1.96 units.

so what I would do is make the following conclusions,
Fcd is the critical cable because it will be the one that carries the highest load. Therefore if the critical load in Fcd is 500N, then Fcd will be 1.96 times higher then Fac

so, Fcd=500=1.96*Fac ==> Fac=500/1.96=255
From simply suming forces in the y dirrection, A must also equal 255.

A good check that i always do is to substitute what you have found back into one (both if you have time but one is usually good enough) equilibrium equations you found in step 2. I actually made a mistake when solving this very problem because I scaled the wrong member but was able to identify my problem when I sub'd my values but into the equilibrium equations.

I hope this is answers your question. You would still be correct in displaying it as ratio (essentially that is what a FBD is anyway, just a comparison of member/support forces), but in my experience with exams I don't display my answers in ratio form ie a:b:c:d as for a structure with more then 3 members I think it would become a little messy.

Elbarto

 

[CharlesL]

Alright the equation Fcd=500=1.96*Fac ==> Fac=500/1.96=255 would be an ideal way to explain my calculation to obtain the weight of A.
Thanks again for showing the way Elbarto.

Charles

 

[elbarto]

No worries mate, glad I could help you out.

Yes in my opinion is the ideal way to show how you concluded that A is 255. The question asks you to find A and theata, so as long as you end up with a solution that at some stage has,
Theata=?
A=?
then as far as I am concerned the question has been answered.

Elbarto