- #1
hqjb
- 40
- 0
2 Questions about statics of rigid bodies
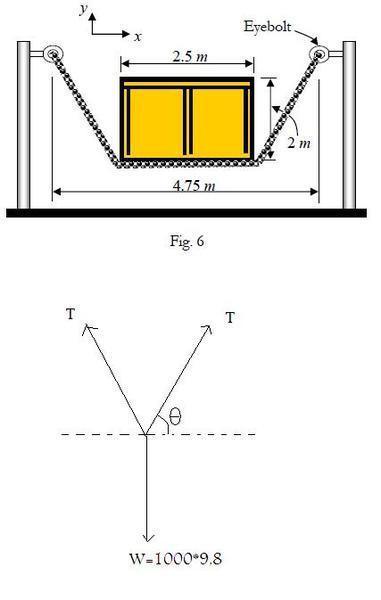
A cable of length 8.5 m is attached to the two posts as shown in Fig. 6. The crate has a mass of 1000 kg. Find the x and y components of the forces exerted by the cable on the eyebolts and find the tension force in the cable.
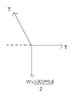
[itex]\theta = \arctan\frac{2}{1.125}[/itex]
[itex]\theta = 60.64[/itex]
[itex]2T\sin 60.64 = 1000 * 9.8[/itex]
[itex]T = 5622.13N[/itex]
[itex]T_x = 5622.13\cos 60.64 = 2756.5N[/itex]
[itex]T_y = 5622.13\sin 60.64 = 4900.5N[/itex]
My question is regarding my free body diagram, I didn't exactly know how to draw it since the box acted its weight not at a point but along a stretch of wire.
So I drew the FBD according to an imaginary point along the centre of gravity concurrent with the cable's tension, is this correct?

This one is really tough, I just need a hint on this problem. All I got was that the pressure would be minimum at r=0m(the centre) and maximum where r=19.6m and theta=0(at the south perimeter).
Not sure how I could find the constants C1 and C2.
Thanks for reading.
Homework Statement
A cable of length 8.5 m is attached to the two posts as shown in Fig. 6. The crate has a mass of 1000 kg. Find the x and y components of the forces exerted by the cable on the eyebolts and find the tension force in the cable.
The Attempt at a Solution
[itex]\theta = \arctan\frac{2}{1.125}[/itex]
[itex]\theta = 60.64[/itex]
[itex]2T\sin 60.64 = 1000 * 9.8[/itex]
[itex]T = 5622.13N[/itex]
[itex]T_x = 5622.13\cos 60.64 = 2756.5N[/itex]
[itex]T_y = 5622.13\sin 60.64 = 4900.5N[/itex]
My question is regarding my free body diagram, I didn't exactly know how to draw it since the box acted its weight not at a point but along a stretch of wire.
So I drew the FBD according to an imaginary point along the centre of gravity concurrent with the cable's tension, is this correct?
Homework Statement
The Attempt at a Solution
This one is really tough, I just need a hint on this problem. All I got was that the pressure would be minimum at r=0m(the centre) and maximum where r=19.6m and theta=0(at the south perimeter).
Not sure how I could find the constants C1 and C2.
Thanks for reading.