- #1
Joosh
- 7
- 4
Hello again, everyone. Have a multivariate calculus question this time around. If anyone can point me in the right direction and help me see where WebAssign finds me wrong, it would be greatly appreciated.
1. Homework Statement
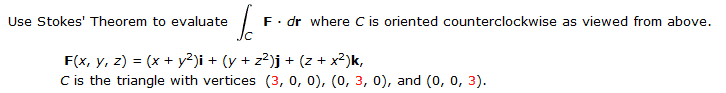
∫∫ScurlF ⋅ dS = ∫CF ⋅ dr
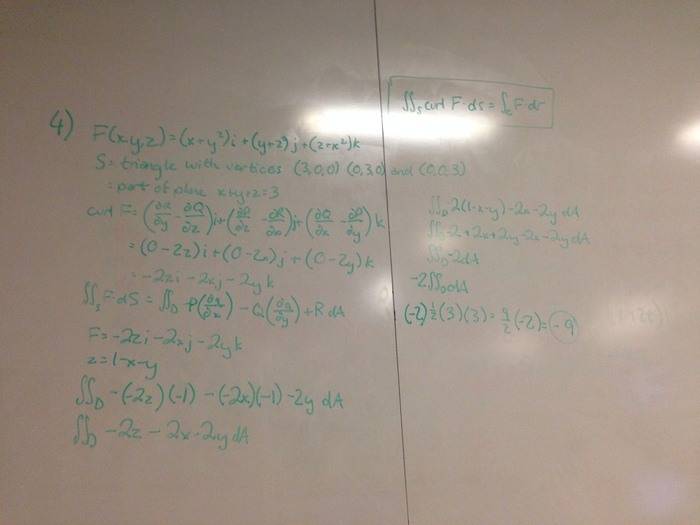
1. Homework Statement
Homework Equations
∫∫ScurlF ⋅ dS = ∫CF ⋅ dr