Strange indefinite integral

[GodsmacK]

Hello, everyone

I've trying to solve this integral but it seems like the methods I know are not enogh to solve it. So I'd be glad if you could give me some trick to get into the answer.
Here it is:

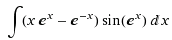
Thanks in advance!

 

[OldEngr63]

Maple knocked it out right away (I have no idea what the details are):

Integral = num/den
where
num =(x*e^x*(tan((1/2)*e^x))^2-x*e^x+2*tan((1/2)*e^x))
den=(1+tan((1/2)*e^x))*e^x

Perhaps having the result in hand will enable you to go back and fill in the gaps.

 

[Charles Stark]

I found it to be e^-xsin(e^x) - xcos(e^x) + c
This was through Wolfram and I would guess integration by parts somehow

 

[GodsmacK]

Hey guys!

I've just solved this thing. In fact, like Charles wrote, it is integration by parts. First you distribute the $\sin(e^x)$ into the parenthesis, then you do the substitution $u=e^x$. After some steps you shall get something like this:

$I=\int \ln(u) \sin(u)du-\int \frac{\sin(u)}{u^2}du$

Applying integration by parts:

$I=-\cos(u) ln(u)+\int \frac{\cos(u)}{u}du+\frac{\sin(u)}{u}-\int \frac{\cos(u)}{u}du$

And there you are... As you see the non-primitive function integral gets cancelled.

 

[Charles Stark]

Eureka! And substituting back reduces it down. Aren't integrals just a blast?