- #1
Paul L
- 8
- 0
The problem:
See attachment for figure.
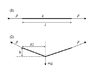
(1) A rope with a spring constant k is stretched by a force F.The length of the rope is l (including the deformation).
(2) A force mg is then applied at l/2 on the rope. This results in a height difference between the highest (and unchanged point) and the lowest point, h. The length between the endpoints where the force F is applied is still l.
Equations:
Hooke's law for springs: F=kx
Maybe something else? Cant see where and what though...
The question:
Set up an equation for the force F.
My attempts:
I've tried to solve this problem with geometric similarity between the force and the deformation, but obviously not correctly...
Applying in real life:
This is thought to be a model of a slack line set up. If you don't know what that is, do a search on flickr.com and you'll get the idea. Is it reasonable to expect that such thing will follow Hooke's law for springs? Is there any other theory that is better to use? Links?
See attachment for figure.
(1) A rope with a spring constant k is stretched by a force F.The length of the rope is l (including the deformation).
(2) A force mg is then applied at l/2 on the rope. This results in a height difference between the highest (and unchanged point) and the lowest point, h. The length between the endpoints where the force F is applied is still l.
Equations:
Hooke's law for springs: F=kx
Maybe something else? Cant see where and what though...
The question:
Set up an equation for the force F.
My attempts:
I've tried to solve this problem with geometric similarity between the force and the deformation, but obviously not correctly...
Applying in real life:
This is thought to be a model of a slack line set up. If you don't know what that is, do a search on flickr.com and you'll get the idea. Is it reasonable to expect that such thing will follow Hooke's law for springs? Is there any other theory that is better to use? Links?