Stress and angle of deflection

[Dell]

A thin- walled tube has been fabricated by bending a metal plate of thickness t into a cylinder of radius c and bending together the edges of the plate. Torque T is then applied to the tube, producing a shearing stress S1 and an angle twist P1 . Denoting by S2 and P1 , respectively, the shearing stress and the angle of twist which will develop if the bond suddenly fails, express the ratios S2/S1 and P2/P1 in term of the ratio c/t

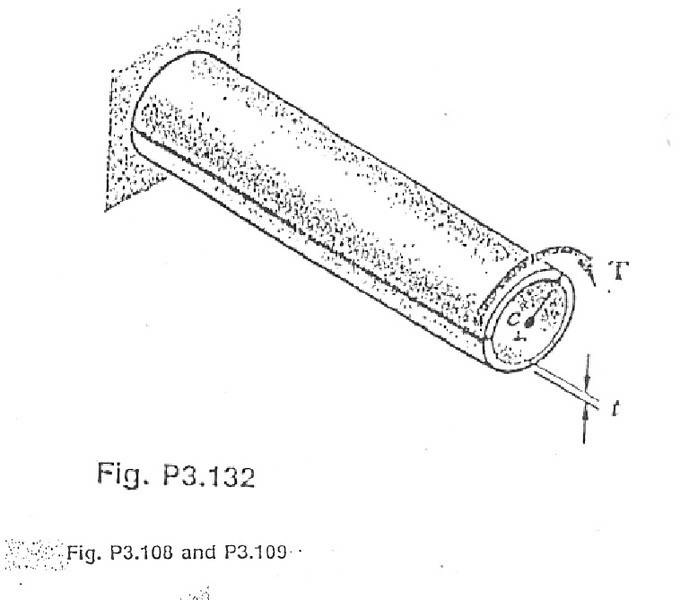
all that i can see here is the obvious,

since it is a thin walled tube i can use the following

$$\tau$$_max=T*r_avg/J
J=2pi*r_avg³*t
dP/dt=T/(GJ)

now i know that r_avg=c+t/2

what i also think is that at point 2, (P2,S2) i am at the critical point of the joint where it reaches its maximum so S2=$$\tau$$_max

but that's all i manage to get and nowehre near any kind of ratio c/t

 

[LightHero]

what am i missing here? The ratios S2/S1 and P2/P1 can be expressed in terms of the ratio c/t as follows:S2/S1 = (c + t/2)^3 / t^2P2/P1 = (c + t/2)^4 / (G*t^3)

 

[Mene]

I would first analyze the given information and equations to understand the relationship between stress and angle of deflection in this scenario. From the given information, it can be inferred that the tube is under torsional stress due to the applied torque. The shearing stress (S1) is directly related to the applied torque (T) and the radius of the tube (c) through the equation \taumax=T*ravg/J, where \taumax is the maximum shearing stress, ravg is the average radius of the tube, and J is the polar moment of inertia.

Next, I would focus on the angle of deflection, which is represented by P1 and P2. P1 is the initial angle of twist due to the applied torque, while P2 is the angle of twist that would occur if the bond suddenly fails. The rate of change of angle of twist (dP/dt) can be calculated using the equation dP/dt=T/(GJ), where G is the shear modulus of the material.

To express the ratios S2/S1 and P2/P1 in terms of the ratio c/t, I would use the equation for J and substitute the values for ravg and t. This would give J=2pi*(c+t/2)^3*t. Then, I would substitute this value of J into the equations for S1 and P1, which would give S1=T/(2pi*(c+t/2)^2*t) and P1=T/(G*2pi*(c+t/2)^3*t).

To find the ratio S2/S1, I would substitute the value of \taumax (which is equal to S2) into the equation for S1. This would give S2/S1=\taumax/(T/(2pi*(c+t/2)^2*t)). Simplifying this further, I would get S2/S1=2pi*(c+t/2)^2/t. Similarly, to find the ratio P2/P1, I would substitute the value of P2 (which is equal to dP/dt) into the equation for P1. This would give P2/P1=dP/dt/(T/(G*2pi*(c+t/2)^3*t)). Simplifying this, I would get P2/P1=G*2pi*(c+t/2)/T.

In conclusion, the ratios S2/S