- #1
'roidbreaker
- 14
- 0
"Stress" around fulcrum
helo,
I have a couple of forces described in f''(t), and the f'(t) yields a momentum vector plane like pic:
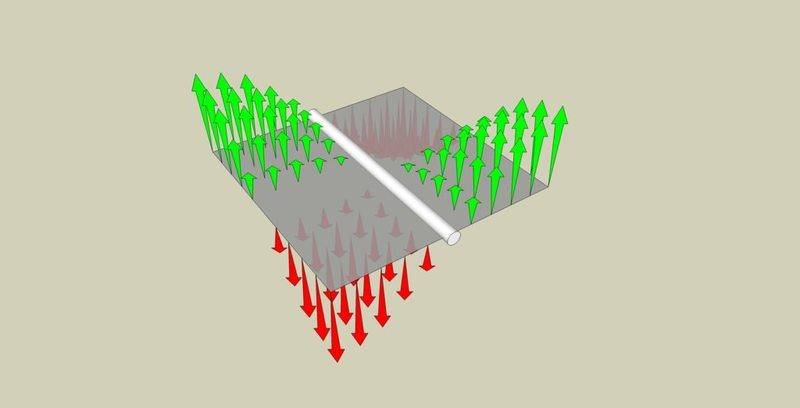
in this picture, we have a solid square plate of some hard material, and an axis where the white rod is.
Since the sum of the vectors on each side equal 0, the square is not rotating. What justification can I give to add -f'(t) to the system and demonstrate that f''(t)+(-f''(t))=0, and from that that the forces in f''(t) neutralize themselves and have no effect as long as the material does not transition into deformation?
Can I just say that the net momentum around the axis is 0 (by adding it all up), and cite conservation of energy?
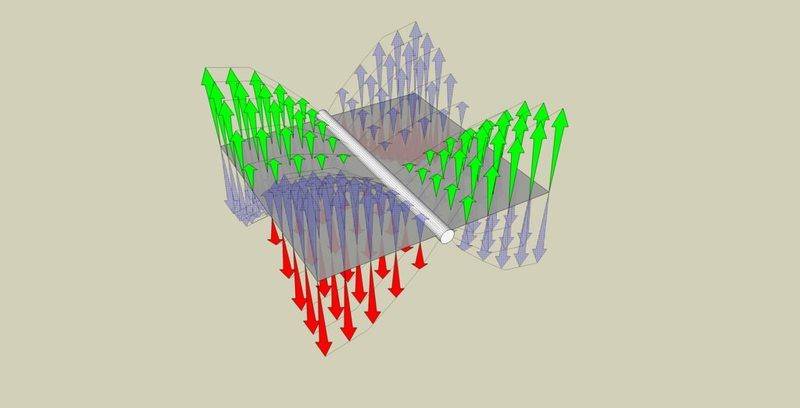
thanks!
helo,
I have a couple of forces described in f''(t), and the f'(t) yields a momentum vector plane like pic:
in this picture, we have a solid square plate of some hard material, and an axis where the white rod is.
Since the sum of the vectors on each side equal 0, the square is not rotating. What justification can I give to add -f'(t) to the system and demonstrate that f''(t)+(-f''(t))=0, and from that that the forces in f''(t) neutralize themselves and have no effect as long as the material does not transition into deformation?
Can I just say that the net momentum around the axis is 0 (by adding it all up), and cite conservation of energy?
thanks!
Last edited: