- #1
- 13,349
- 3,115
Yes, one more reason to be humble, I know. This is the simplest problem I couldn't solve so far.
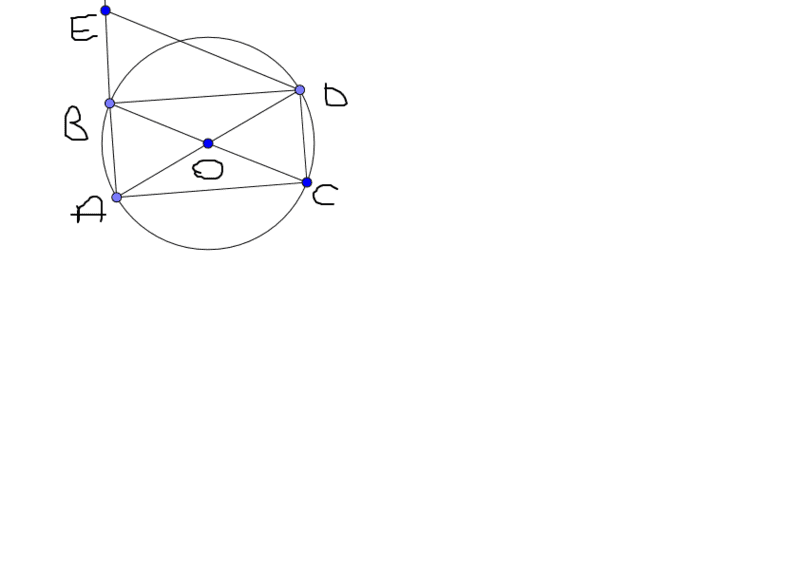
Assume we have a circle of center O, a ruler of arbitrary size and a pencil.
We use the ruler and the pencil to choose 4 points on the circle - the extremities of two diametral/diagonal segments.
They build a rectangle. So far so good.
Using the ruler only and the pencil, how can I draw the segment ED (with E the intersection of a line passing through D and the prolongation of AB) which is parallel to the diagonal segment BC?
Thank you for illuminating me.
Assume we have a circle of center O, a ruler of arbitrary size and a pencil.
We use the ruler and the pencil to choose 4 points on the circle - the extremities of two diametral/diagonal segments.
They build a rectangle. So far so good.
Using the ruler only and the pencil, how can I draw the segment ED (with E the intersection of a line passing through D and the prolongation of AB) which is parallel to the diagonal segment BC?
Thank you for illuminating me.
 Unfortunately, I think this violates the rules: the ruler is of arbitrary length, but not arbitrary width. For completeness, here would be the rest of the solution:
Unfortunately, I think this violates the rules: the ruler is of arbitrary length, but not arbitrary width. For completeness, here would be the rest of the solution: