- #1
roam
- 1,271
- 12
- TL;DR Summary
- Empirically we know that if we add ##N## signals with independent random phases and amplitudes, the shape of the sum flattens out as ##N## tends to infinity. How can this effect be formally demonstrated?
For instance, here is an example from my own simulations where all underlying signals follow the same analytical law, but they have random phases and amplitudes (such that the sum of the set is 1). The thick line represents the sum:
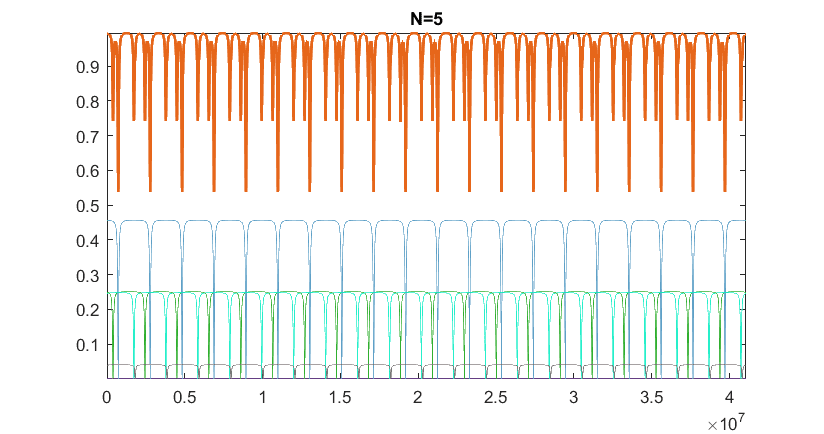
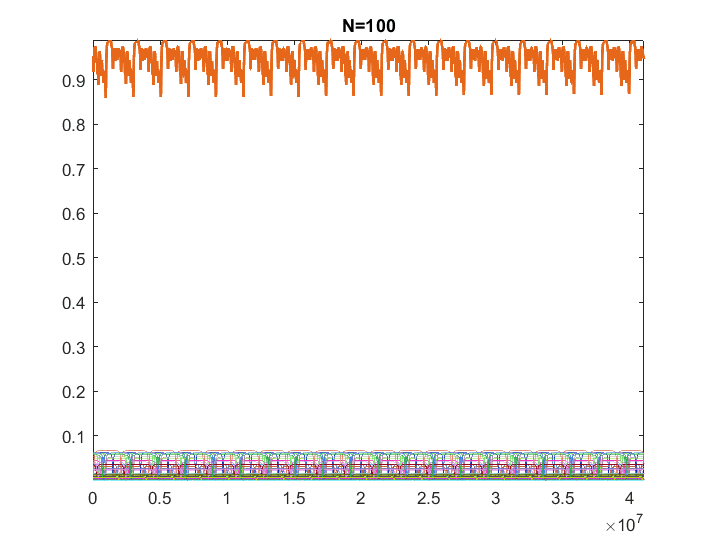
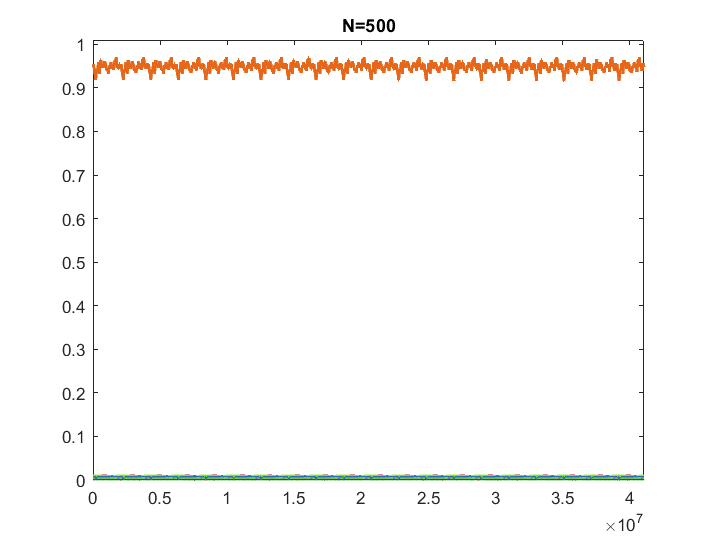
Clearly, the sum tends to progressively get flatter as ##N \to \infty##. Is there a formal mathematical way to show/argue that as the number of underlying components increases, the sum must tend to a flat line?
Clearly, the sum tends to progressively get flatter as ##N \to \infty##. Is there a formal mathematical way to show/argue that as the number of underlying components increases, the sum must tend to a flat line?