- #1
Jackson Lee
- 77
- 1
The superposition of sound waves puzzled me. Just like the figure below, when two loudspeakers propagate sound waves from two locations to any other locations. We always calculate final wave's amplitude or intensity via considering something just like phase difference or change of amplitude, but we never take into account the angle between the propagation directions. Sound wave is longitudinal wave, thus I suppose the superposition of amplitude should be the superposition of vectors. If it is so, then the final intensity calculation should be done this too. However, it seems that few textbook ever did this. If it is not sound waves but light wave or other electromagnetic waves, it is definitely correct because they are transverse waves. When we calculate final amplitude, we could neglect angles. But we could do this for sound waves?
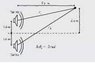
![20140909_092524[1].jpg](/data/attachments/56/56044-587941692984640d6e778f4ca10e9677.jpg)
