Optimal Launch Speed for Swinging Across a Ravine

[Iconic]

Homework Statement

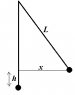
A hiker plans to swing on a rope across a ravine in the mountains, as illustrated in the figure, where L = 4.0 m and x = 1.8 m, and to drop when she is just above the far edge. At what minimum horizontal speed should she be moving when she starts to swing(in m/s)?

Homework Equations

E_i= E_f
So...
Ke = Pe
So...
1/2mv²=mgh

The Attempt at a Solution

I have the equation set up correctly but I just don't know how to find h so I can find V

1/2mv²=mgh

The Rope makes a isosceles triangle shape so I thought of L as adjacent, and X as the Opposite so I could solve for theta by doing Θ = arctan(1.8/4.0) = 24.22º. However, upon looking at the answer online- it says to take the arcsin(1.8/4.0) = 26.7º. Why is this?

 

[TSny]

$L$ is not the side adjacent in the right triangle.

 

[Simon Bridge]

For that matter, x is not the base of an isosceles triangle, as TSny's diagram illustrates.
That is not the formula for finding the apex angle of an isosceles triangle anyway.
As TSny says: $x\neq L\tan\theta$ either.

I'm kinda puzzled that they want you to find the angle at all.
Since you know L and x, why not find h by pythagoras?