- #1
Dell
- 590
- 0
given a symmetrical truss, loaded with an assymetrical load, i can divide this truss into 2 separate symmetrical trusses, one with a symmetrical load and one with an antisymmetrical load, then to solve the truss i can solve half of each of these 2 trusses and add/subtract results accordingly.
when i draw the left hand side of each of these trusses what supports do i add at the central line?? as far as i know, the symmetrical truss can have a "y" deflection at this point but the antisymmetrical truss cannot, so i add a support with an 'x' axis reaction to the symmetrical and a "y" reaction to the antisymmetrical
my question is how many supports do i need to add? in all the examples i have seen supports have been added at the corners,- as seen in this example
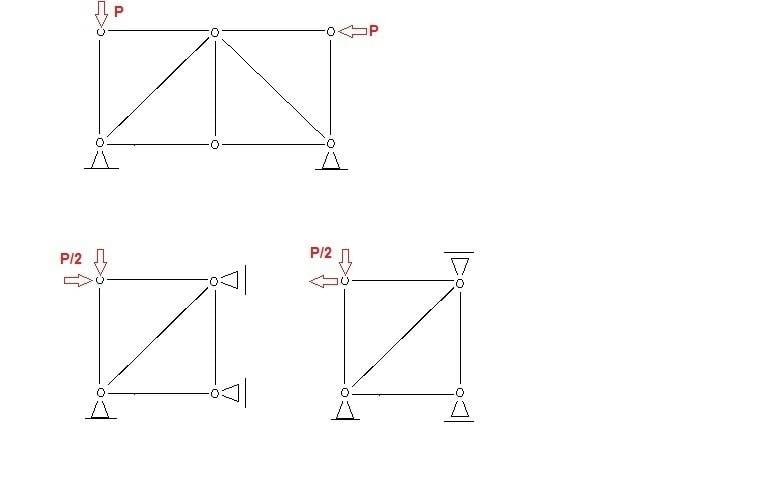
but i think that adding just one of the supports (top right ) would do the trick as far as the deflection restraints are concerned..
also i have seen in examples with structures other than trusses, sometimes the central bar(if there is one) is ignored completely in the symmetrical half. why is this??
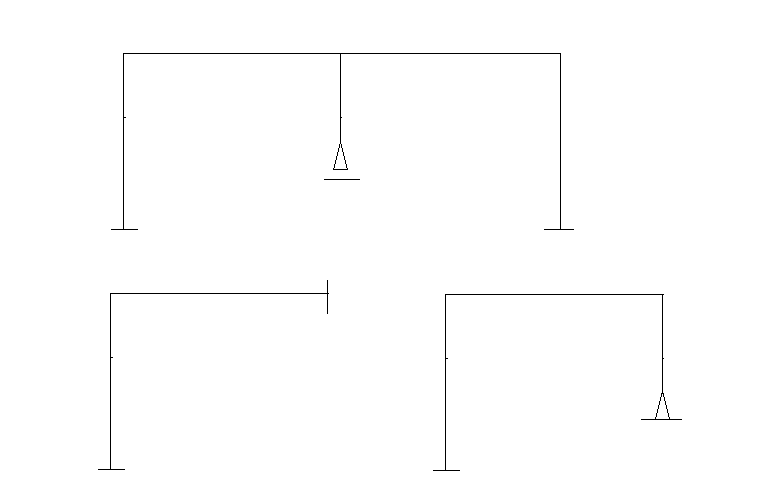
when i draw the left hand side of each of these trusses what supports do i add at the central line?? as far as i know, the symmetrical truss can have a "y" deflection at this point but the antisymmetrical truss cannot, so i add a support with an 'x' axis reaction to the symmetrical and a "y" reaction to the antisymmetrical
my question is how many supports do i need to add? in all the examples i have seen supports have been added at the corners,- as seen in this example
but i think that adding just one of the supports (top right ) would do the trick as far as the deflection restraints are concerned..
also i have seen in examples with structures other than trusses, sometimes the central bar(if there is one) is ignored completely in the symmetrical half. why is this??