Discussion Overview
The discussion revolves around the temperature of gas produced during water electrolysis, specifically how to calculate it given certain parameters such as moles, volume of the container, and energy input. Participants explore the relationship between the energy used for electrolysis and the heating of both water and gas, as well as the implications of system constraints.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants propose using the specific heat capacity formula to find the temperature of water during electrolysis, given mass, specific heat constant, and energy input.
- Others argue that part of the energy is used for splitting water, complicating the calculation of temperature for the gas produced.
- A participant suggests subtracting the mass of gas produced from the initial mass of water to find the remaining mass for calculations.
- Another participant emphasizes that energy input is used for both water decomposition and heating, and that calculating final temperatures in a closed system is complex.
- There is a discussion about combining specific heat capacities of water and gas to calculate the overall heat capacity of the system.
- One participant expresses confusion about the relationship between heat capacity and specific heat capacity, leading to further clarifications from others.
- Participants discuss the importance of using correct units and notation in calculations, with some corrections made throughout the thread.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to calculate the temperature of the gas produced during electrolysis. There are multiple competing views on how to account for energy distribution between heating and decomposition, and the discussion remains unresolved.
Contextual Notes
Participants highlight the need for precision in definitions and calculations, particularly regarding mass versus volume and the use of specific heat versus heat capacity. There are unresolved mathematical steps and assumptions about system conditions that affect the calculations.
Who May Find This Useful
This discussion may be useful for individuals interested in thermodynamics, electrolysis processes, and the calculations involved in energy transfer and temperature changes in chemical systems.

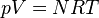 But what if I only know the moles, volume of the container, and joules added? Any help would be greatly appreciated!
But what if I only know the moles, volume of the container, and joules added? Any help would be greatly appreciated!