- #1
snormanlol
- 5
- 2
- Homework Statement
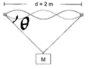
- A mass M (15kg) is hanging on a string which is forming a closed loop (total length of the loop = 5m, with mass per unit length=2*10^(-3) kg/m). The string runs trough 2 mass and frictionless wheels, with a distance of 2 meters between them. Determine the tension T in the string.
- Relevant Equations
- F = m*a;
τ=I*α
I know that the answer has to be 98.6N. So I know that Fy=0 so that 2*T*sin(theta) = 147.25. Then I was think to take the torque of the left wheel but I can't find the lever arm of the tension force. I also know that u can solve the question by saying that the 2 sides of unknown length are 1.5 m but I'm not sure why u can do that.
Here is a picture of the problem:
Here is a picture of the problem: