- #1
pinokicake
- 8
- 0
Homework Statement
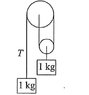
Two masses hang by a pulley system shown in the attachment. The masses both weigh the same. Find the tension on the rope.
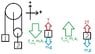
The first attachment is straight from the book, the second attachment is me redrawing it with labels along with a free body diagram of each mass (vectors not to scale) and the third is another picture with labeled ropes (its relevance is in the explanation of my thinking under "attempt at solution").
Homework Equations
m1 = mass on the left a1 = acceleration of m1
m2 = mass on the right a2 = acceleration of m2
m1 = m2 = m
T = tension
F = ma
Weight = mg
Ideal Mechanical Advantage (IMA) = Fout/Fin
4. The answer provided
The answer is 3/5mg. I will go into how they arrive to this in #5
4. The attempt at a solution
Alright, I know my main problem is this figuring out which mass I designate the input force and which i designate the output force.
My first attempt was saying the the input force would be where m1 hangs and the output force would be where m2 hangs. I also know that with a pulley, the mechanical advantage is the amount of strings supporting movable pulley. So with that said:
2 = Fout/Fin
2 = ma2/ma1
2 = a2/a1
2a1 = a2 this is where my mistake is, the book claims that m1 should be moving twice as fast as m2 or in other words a1 = 2a2.
Now I understand that this should be true. In the third attachment I labeled all three ropes starting with the left most rope 1, 2 and 3. If rope 1 were to lengthen a total of 2 meters, both ropes 2 and 3 need to shorten a total of 1m. This would mean that m1 would move down 2m and m2 would move up 1m. Both the masses are moving at the same time, so for each mass to move to their respected heights, m1 needs to go twice as fast as m2 (it has to cover twice as much distance as m2).
5. The worked solution
With the correction in mind the following is the worked solution to the problem:
-F1 = -ma1 = T - mg
F= ma1 = mg - T
a1 = 2a2
2ma2 = mg - T
F2 = ma2 = 2T - mg
a2 = (2T - mg)/m
2m[(2T - mg)/m] = mg - T [on the left side of the equation m in the denominator cancels and we distribute the 2]
4T - 2mg = mg -T
5T = 3mg
T = 3/5mg