Finding Tension in Rotating Rod: What is the Function of T(x)?

[manasi bandhaokar]

a thin uniform rod of length l and density d is rotating with angular velocityω about an axis passing through one of its ends and perpendicular to it.find the tension int the rod as a function of x.(x= dist from axis of rotation).area of cross section = a

attempt at solution:

consider a small of length dx at dist x from axis.

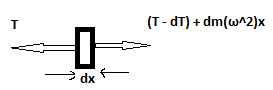
for equilibrium of rod T = T-dT + dmω^2 x
dT = dm ω^2 x
integrating
T(x) =(d * a* ω^2 (x^2 - l^2))/2
this is negative of answer.where am i wrong?

 

[FranzDiCoccio]

I guess that $a$ and $d$ are the cross-sectional area and the density of the rod, respectively.

Your second equation, the one for $dT$, seems ok to me. I do not understand how can you obtain your last result from it. What are the limits of your integral?
Seems to me you're missing a sign in the integration, or, equivalently, you are swapping the integration limits.

 

[haruspex]

Further to @FranzDiCoccio 's comments, since it is a thin rod I would interpret "density" as meaning mass per unit length. You do not need a variable for the cross sectional area.

 

[TSny]

for equilibrium of rod T = T-dT + dmω^2 x
dT = dm ω^2 x
integrating
T(x) =(d * a* ω^2 (x^2 - l^2))/2
this is negative of answer.where am i wrong?

I think the problem is associated with the minus sign in writing T - dT for the tension at the outer end of dx. The change in the function T(x) as you go from x to x + dx should be written as dT not - dT. The change in the function will be a negative quantity. So, the value of T at x+dx is T + dT where dT is a negative quantity.

By writing the tension at x + dx as T - dT, your symbol dT does not represent the change in the function T(x), it's the negative of the change in T(x).

 

[manasi bandhaokar]

I think the problem is associated with the minus sign in writing T - dT for the tension at the outer end of dx. The change in the function T(x) as you go from x to x + dx should be written as dT not - dT. The change in the function will be a negative quantity. So, the value of T at x+dx is T + dT where dT is a negative quantity.

By writing the tension at x + dx as T - dT, your symbol dT does not represent the change in the function T(x), it's the negative of the change in T(x).

oh!
thanks!