- #1
Daascc
- 6
- 0
Homework Statement
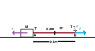
A box weighs 12.6kg and it is dragged with a rope(it weighs 1.4kg and the length is 60cm).The force dragging the box is F=80N.The coefficient of kinetic friction is 0,5.
What is the tension of the rope in the middle?(Answer:17N)
Homework Equations
No revelant equations
The Attempt at a Solution
(F-T=m2 (1.4kg)*a;T-md (kinetic friction)*m1(12.6kg)*g)
T=78N but it is wrong.