Tension on a string during SHM

[QuarkCharmer]

Homework Statement

a 0.12kg mass is suspended on a magic string with no mass, and length of 0.80m. There is no air resistance, and the pendulum is swinging such that it makes a maximum angle of 45 degrees with the vertical.

A.) What's the speed as it passes the vertical position?
B.) What is the tension in the string when it makes an angle of 45 with the vertical?
C.) What is the tension in the string as it passes through the vertical?

Homework Equations

The Attempt at a Solution

A.) I simply used the conservation of energy to determine it's velocity at the bottom:
$$mgh = \frac{1}{2}mv^{2}$$
$$gh = \frac{1}{2}v^{2}$$ //masses cancel
$$\sqrt{2(9.8)h} = v$$

$h = (.80)-(.80)cos(45)$

$$\sqrt{2(9.8)((.80)-(.80)cos(45))} = v$$
$$v=2.1 m/s$$

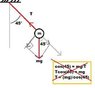
B.) Here is what I tried:

$$T = \frac{mg}{cos(45)}$$
$$T = \frac{(0.12)(9.8)}{cos(45)}$$
$$T = 1.66 N$$
Which is wrong for some reason. I believe the solution to be mgsin(45) but I don't understand why?

 

[ehild]

The tension points toward the hinge. Gravity can be decomposed into components parallel with the string and perpendicular to it.

ehild

 

[QuarkCharmer]

Aren't I only concerned with the red vectors in this image? Since the mass has reached it's max height and velocity/acceleration are zero at this point. I figured that there must be another vector canceling out the green mgcos(45), leaving only the red mgcos(45) to be equal to the tension as per Newton's third?

I'm still not seeing where a sine comes into play here.

 

[Matterwave]

You drew the tension in the wrong way in the first figure. At the top of the pendulum's trajectory, the velocity is 0, and so is the force in the direction along the string. You must balance the tension and the gravitational force (projected into that direction).

 

[QuarkCharmer]

You drew the tension in the wrong way in the first figure. At the top of the pendulum's trajectory, the velocity is 0, and so is the force in the direction along the string. You must balance the tension and the gravitational force (projected into that direction).

I drew it that way because it would be equal to the vector in the direction of the string that represents tension.

 

[Matterwave]

What I'm saying is...T and mg do not make two legs of a triangle like in that figure, I think that's why you're getting confused and writing cos(45)=mg/T or something like that.

 

[ehild]

Aren't I only concerned with the red vectors in this image? Since the mass has reached it's max height and velocity/acceleration are zero at this point.

The velocity is zero, but the acceleration is not. The component of gravity which is normal to the string accelerates the body, while the tension is equal to the parallel component of gravity (as the centripetal force is zero).

ehild

 

[QuarkCharmer]

I see my previous problem, I don't know what I was thinking!

Now I am attempting to find the Tension on the string through the vertical (zero degrees).

I was thinking that since mg pulls down on the mass, T pulls up, and there are no other forces in the y direction, that the solution would simply be mg.

But, to get the right solution I applied F=ma and substituted in v^2/r for a, giving me..
$$T-mg = m\frac{v^{2}}{L}$$
Which produced the correct answer, but it is just really non intuitive how acceleration works in circular motion (a section we briefly discussed but did no actual problems on so I am going to go back and do problems there in more detail). What is the idea with this thinking?

 

[ehild]

2

I was thinking that since mg pulls down on the mass, T pulls up, and there are no other forces in the y direction, that the solution would simply be mg.

But, to get the right solution I applied F=ma and substituted in v^2/r for a, giving me..
$$T-mg = m\frac{v^{2}}{L}$$
Which produced the correct answer, but it is just really non intuitive how acceleration works in circular motion (a section we briefly discussed but did no actual problems on so I am going to go back and do problems there in more detail). What is the idea with this thinking?

The object moves along a circle of given radius R(=L) and speed v. That can only be if an appropriate centripetal force acts on it pointing to the centre. The radial components of all forces have to sum up to give the centripetal force:

∑F_r=mv²/R

As the direction of the velocity changes when moving along a circle, there is acceleration towards the centre (see this video http://www.youtube.com/watch?v=fSfVVz0eIis:) It is called the centripetal acceleration a_cp and ia_cp= v₂R. You will learn how to derive this expression.

ehild