- #1
doctorjanitor
- 7
- 0
I can't really follow the template with this question.
Im dropping parachutes out of a window with weights attatched. I'm assuming that they travel at terminal velocity from the moment i drop them, and i know this becomes less and less true the heavier weights i use.
I plotted the results i got as weight (Newtons) against terminal velocity (m/s).
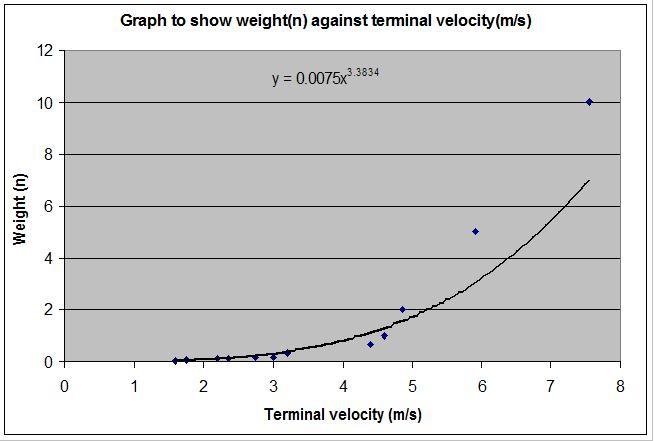
The lightest weight i dropped was 0.048 Newtons, and the heavest was 10. This makes this graph imossible to see any results from and i know that nothing above 30ish Newtons reached terminal velocity.
I worked out the resistive force, and when it was equal to the weight, i knew they had reached terminal velocity. Below is the graph that focuses on the drops that reached terminal velocity.
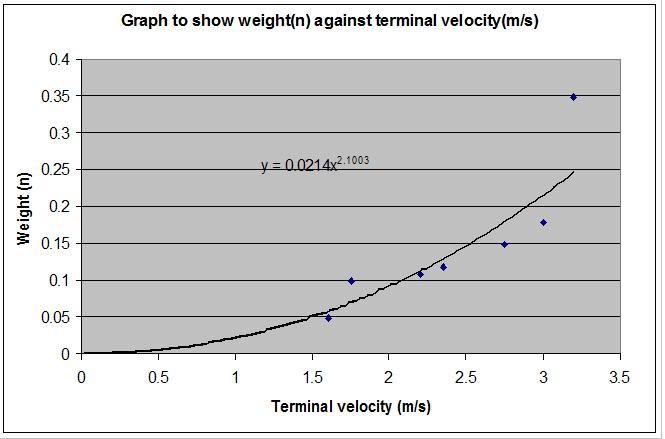
Now from that graph, it is not clear wether the graph should be linear or curved. If it is linear it will cross the X axis at around 1 m/s, is that pheasable? Would it travel at 1 m/s?? with extremely small mass? I think my result / trend line falls appart at lower weights but i am still not sure of the line of best fit.
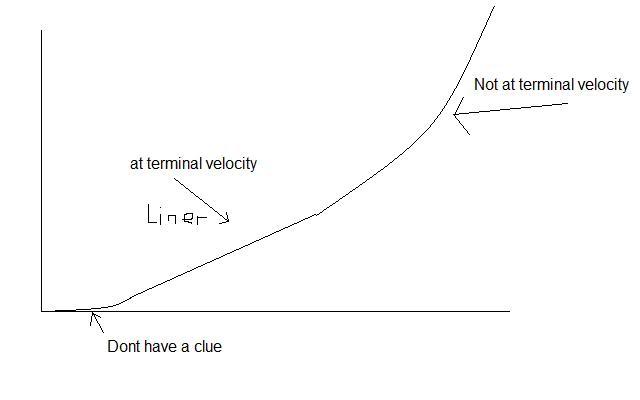
You can ignore the last point on the second graph as that is questionable as to wether it reaches terminal velocity or not. I think that the graph might be linear where the results reach terminal velocity, and when the weights don't reach terminal velocity the graph is curved, but i also don't know if this is right. Can anyone add any insight to my investigation on what you think the results show? Just a little bit stuck that's all.
Maybe it should look like this:
Thanks a lot for your time!
Im dropping parachutes out of a window with weights attatched. I'm assuming that they travel at terminal velocity from the moment i drop them, and i know this becomes less and less true the heavier weights i use.
I plotted the results i got as weight (Newtons) against terminal velocity (m/s).
The lightest weight i dropped was 0.048 Newtons, and the heavest was 10. This makes this graph imossible to see any results from and i know that nothing above 30ish Newtons reached terminal velocity.
I worked out the resistive force, and when it was equal to the weight, i knew they had reached terminal velocity. Below is the graph that focuses on the drops that reached terminal velocity.
Now from that graph, it is not clear wether the graph should be linear or curved. If it is linear it will cross the X axis at around 1 m/s, is that pheasable? Would it travel at 1 m/s?? with extremely small mass? I think my result / trend line falls appart at lower weights but i am still not sure of the line of best fit.
You can ignore the last point on the second graph as that is questionable as to wether it reaches terminal velocity or not. I think that the graph might be linear where the results reach terminal velocity, and when the weights don't reach terminal velocity the graph is curved, but i also don't know if this is right. Can anyone add any insight to my investigation on what you think the results show? Just a little bit stuck that's all.
Maybe it should look like this:
Thanks a lot for your time!