The highest possible potential in a van de Graaf generator

[Order]

Homework Statement

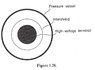
Figure 1.26 (will describe it later on) shows a cross section of a van de Graaf generator, surrounded by an 'intershield' and a pressure vessel, both of which are also cylindrical. The gas in the pressure vessel breaks down in Electric fields greater than 1.6×10⁷ volts/m. If the radii of the terminal, intershield and pressure vessel are a=1.5 m, b=2,5 m and c=4 m respectively, what is the highest potential difference that can be maintained between the terminal and the pressure vessel? (Hint: the intershield must be maintained at a potential such that breakdown is about to occur on its own outer Surface as well as on the Surface of the terminal.)

Homework Equations

$$\int_{S} \textbf{E} \cdot d \textbf {S} = \frac{q}{\epsilon_{0}}$$
$$\phi (\textbf{r}_{B}) - \phi (\textbf{r}_{A}) = \int_{A}^{B} \textbf{E} \cdot d \textbf{l}$$

The Attempt at a Solution

I evaluate the Surface integral over a length l>>b of the cylinder where i suppose the field will break down. That is I suppose $E_{max}=E_{b}$
$$\int_{S} \textbf{E}_{max} \cdot d \textbf {S} = E_{max} \pi b^{2} l = \frac{q}{\epsilon_{0}}$$
At any Point outside the inner terminal
$$\int_{S} \textbf{E} \cdot d \textbf {S} = E(r) \pi r^{2} l = \frac{q}{\epsilon_{0}}$$
combining these two equations i arrive at
$$\textbf{E} = E_{max} \frac{b^{2}}{r^{2}} \hat{r}$$
And evaluating the potential
$$\Delta \phi = - \int_{a}^{c} E_{max} \frac{b^{2}}{r^{2}} dr = E_{max} b^{2} \left( \frac{1}{c}-\frac{1}{a} \right) = 41 MV$$
But the answer should be 31 MV.
What I don't understand in the hint is that breakdown should occur at two places at once. This must be impossible because the Electric field should be higher Close to the cylinder Before there is breakdown at the intershield (Point b).

ps. sorry that I don't know how my scanner works but I Think the generator i described in the text. ds.

 

[rude man]

I would need to see the picture. Is the intershield connected to anything?

 

[Order]

Here is the picture

I would need to see the picture. Is the intershield connected to anything?

I guess it is not, rude man. It is just the first chapter of the book. Look for yourself.

 

[rude man]

I guess it is not, rude man. It is just the first chapter of the book. Look for yourself.

Well, the given hint seems to suggest that the intershield is held at a certain potential rather than it just assumes whatever potential it would if it were floating ... on the other hand, no voltage connection between the terminal and the intershield is shown ... I'll try to think about it.

 

[Order]

Well, the given hint seems to suggest that the intershield is held at a certain potential rather than it just assumes whatever potential it would if it were floating ... on the other hand, no voltage connection between the terminal and the intershield is shown ... I'll try to think about it.

Ok, suppose then that it does. Then I know that between b and c the Electric field is $$E_{outside b}=E_{max} \frac{b^2}{r^2}$$
according to my previous calculations. But what is the field inside the intershield? When I use Gauss law right outside the terminal (Point a) and right outside the intershield (Point b) i get
$$\int_{r=a} \textbf{E} \cdot d \textbf{S} = E_{max} \pi a^2 l = \frac{q_{terminal}}{\epsilon_0}$$
$$\int_{r=b} \textbf{E} \cdot d \textbf{S} = E_{max} \pi b^2 l = \frac{q_{terminal}+q_{intershield}}{\epsilon_0}$$
From this I then can evaluate $q_{intershield}=E_{max} l \pi \epsilon_0 (b^2-a^2)$. I then see that the volume of the intershield at a Point r (between a and b) is $V(r) = l \pi r^2 - l \pi a^2$. Specifically $V(b) = l \pi (b^2 - a^2)$. So from this it is easy to see that the charge density for the intershield must be
$$\rho =\frac{q_{intershield}}{V(b)} = E_{max} \epsilon_0$$
Now I can use Gauss law at a Point r in the intershield
$$\int_{intershield} \textbf{E} \cdot d \textbf{S} = \frac{q_{terminal}+V(r) \rho}{\epsilon_0} = \frac{q_{terminal}}{\epsilon_0}+E_{max} l \pi (r^2-a^2) = E_{max} l \pi r^2$$
But according to this the field inside the intershield is constant! Arriving at this I really felt I must be wrong, but anyway just let me assume I am right and see what the potential is.
$$\Delta \phi_{intershield}=E_{max}(b-a)=16.0 MV$$
$$\Delta \phi_{pressurevessel} = E_{max} b^2 (1/b+1/c)=15.0MV$$
So the total potential difference is 31.0 MV, which is incorrect. The right answer is 31.1 MV and over the intershield it should be 18.8 MV not 16.0 MV. Maybe you have an idea of where I am making false assumptions?

 

[rude man]

OK, I have to make a couple of assumptions:

1. the generator is cylindrical, length L. That seems to be given.
2. Breakdown occurs in the region b to c since that's where the gas is seemingly located. That means I don't understand why the hint talks of breakdown at the terminal. The E field in the gas region b --> c will obviously be greatest at the outer surface of the shield.
3. The intershield is fixed at some potential V2. Call the terminal voltage V1 and the outer vessel potential = 0. So V1 > V2 > 0.

The following is just a suggestion. I'm not sure it's right:

Use Gauss' law to
1. express Qmax on the terminal in terms of Emax at the shield.
2. express V1 - V2 in terms of Q and the geometry.
3. express V2 same way.
4. add 2 and 3 to get V1 which is what you're looking for: a function of Emax and geometry. I assumed that ε of the gas = ε₀ but it's not necessary. Makes things a little bit simpler.

 

[Order]

OK, I have to make a couple of assumptions:

1. the generator is cylindrical, length L. That seems to be given.
2. Breakdown occurs in the region b to c since that's where the gas is seemingly located. That means I don't understand why the hint talks of breakdown at the terminal. The E field in the gas region b --> c will obviously be greatest at the outer surface of the shield.
3. The intershield is fixed at some potential V2. Call the terminal voltage V1 and the outer vessel potential = 0. So V1 > V2 > 0.

The following is just a suggestion. I'm not sure it's right:

Use Gauss' law to
1. express Qmax on the terminal in terms of Emax at the shield.
2. express V1 - V2 in terms of Q and the geometry.
3. express V2 same way.
4. add 2 and 3 to get V1 which is what you're looking for: a function of Emax and geometry. I assumed that ε of the gas = ε₀ but it's not necessary. Makes things a little bit simpler.

Thanks for your help, although I don't get much farther anyway. About your assumptions:
1. I assume L>>a,b or c so that the corrections are small. To evaluate the full integral should be done by a computer or a mathematician :)
2. This seems to be a matter of knowns and unknowns. There are two unknowns: Q_terminal and Q_intershield so therefore we better have to know the field at two Points.
3. This seems fair.

Now I run into problems doing the calculations.
1. I find that $$\int_{shield} \textbf{E} \cdot d \textbf{S} = \frac{Q_{max}+Q_{intershield}}{\epsilon_0} \approx E_{max} \pi b^2 L$$
and thus
$$Q_{max}=\epsilon_0 E_{max} \pi b^2 L - Q_{intershield}$$
There is an annoying unkown Q_intershield here.
2-4. I don't know the field so how can I express any potential difference? With one unknow variable this seems ungainly.
So this problem seems like much more trouble than I anticipated. I had hoped to finish the chapter this week. But...

 

[voko]

The intershield is a third electrode in an advanced van der Graaff generator. It is held at a potential such that the gas between it and the outer tank is at the break-down limit. The same gas is inside, and again the inner terminal is held at a potential such that the gas between it and the intershield is about to break down, exactly as the hint indicates.

 

[rude man]

Voko seems familiar with such a device and the fact that the gas surrounds the entire volume makes sense of the hint.

So the potential of the shield is adjusted until breakdown nearly occurs simultaneously between (1) the terminal and inner shield, and (2) the outer shield and containment vessel.

 

[voko]

Not first hand familiarity, mind you. Just remember reading a book on electrostatic accelerators a while ago. So could be wrong, but, given the hint, not very likely so.

The basic idea is that with just two electrodes, only a very small portion of the gas is stressed. With additional electrodes in between, one can step up the voltage, stressing more of the gas and getting higher voltage overall.

 

[Order]

Yes it is very clever (the Van de Graaf generator), you can have a potential difference over the intershield while the field remains constant. This according to my calculations which however seems to be wrong somehow.
Obviously clever rude man knows something and tries to tell me, but I just don't get it. I have no idea of what is wrong with my reasoning and the difference he tries to suggest. So I guess I have to go on to other problems. At least I was Close to the right answer!

 

[voko]

The electric field of an infinite cylinder is $E(r) = \frac {\lambda} {2 \pi \epsilon_0 r } = \frac {e} {r}$, where $\lambda$ is the charge per unit length, and the potential difference between two cylinders is $V(r_1, r_2) = e \ln \frac {r_2} {r_1}$. So if the field at in inner cylinder is $E$ (the break-down limit), then the potential difference is $E r_1 \ln \frac {r_2} {r_1}$. For three cylinders this yields $E ( r_1 \ln \frac {r_2} {r_1} + r_2 \ln \frac {r_3} {r_2})$.

 

[Order]

The electric field of an infinite cylinder is $E(r) = \frac {\lambda} {2 \pi \epsilon_0 r } = \frac {e} {r}$, where $\lambda$ is the charge per unit length, and the potential difference between two cylinders is $V(r_1, r_2) = e \ln \frac {r_2} {r_1}$. So if the field at in inner cylinder is $E$ (the break-down limit), then the potential difference is $E r_1 \ln \frac {r_2} {r_1}$. For three cylinders this yields $E ( r_1 \ln \frac {r_2} {r_1} + r_2 \ln \frac {r_3} {r_2})$.

Right, I Always assumed the field should be continuous and that the intershield had an even charge distribution but since your solution is correct; I was wrong. I just found the ln-function in my own calculations but since I made a false assumption it did no good. I only had the second term of the potential difference right.

So the charge was at the outer Surface of the intershield all along. Oh if someone had told me!

But wait a minute! If the (say) positive charge is on the outer Surface of the intershield, where is the negative charge? If it is on the inner Surface then your first term equation can't be right, since the field at the (inner part of the cylinder) Surface is not $E$. Does anyone understand my problem?

 

[voko]

I think my notation is somewhat confusing. E, as opposed to E(r), is the constant break-down electric field just outside the terminal and just outside the intershield. The field is different elsewhere.

 

[rude man]

OK, new picture:
potential on terminal = V1. Potential on shield = V2. Potential on container = 0.

So we have Q1 on the terminal and -Q1 on the inner shield surface, and
E1 between a and b = Q1/2πεLr and by integration Q1 = 2πεL(V1-V2)/ln(b/a).

Similarly, we have -Q2 on the container vessel and Q2 on the outer shield surface, so
E2 between b and c = Q2/2πεLr and by integration Q2 = 2πεLV2/ln(c/b).

Knowing Q1 and Q2 you know the E field adjacent to the terminal and the outside shield surface. Equate them and set them equal to Emax and you can solve for V1 and V2.

What's interesting is the shield has finite charge Q2 - Q1 on it.

Hope this clicks.

 

[Order]

OK, new picture:
potential on terminal = V1. Potential on shield = V2. Potential on container = 0.

So we have Q1 on the terminal and -Q1 on the inner shield surface, and
E1 between a and b = Q1/2πεLr and by integration Q1 = 2πεL(V1-V2)/ln(b/a).

Similarly, we have -Q2 on the container vessel and Q2 on the outer shield surface, so
E2 between b and c = Q2/2πεLr and by integration Q2 = 2πεLV2/ln(c/b).

Knowing Q1 and Q2 you know the E field adjacent to the terminal and the outside shield surface. Equate them and set them equal to Emax and you can solve for V1 and V2.

What's interesting is the shield has finite charge Q2 - Q1 on it.

Hope this clicks.

You are very patient in trying to explain this for me. I have solved all the other problems in the chapter but I still have difficulties with this, which is one of the first. I don't have problems in doing the maths, it is just that I don't understand the physics when solving it. But from what I read in your (rude man's) post I have made a picture (see picture attached to this post). According to this picture I get the outer potential difference right:
$$\int_{vessel} \textbf{E} \cdot \textbf{S} =Q_2 / \epsilon_0 = E_{max} \pi 2 b L = E(r) \pi 2 r L$$
which with integration leads to
$$\Delta \phi_{vessel} = E_{max} b \ln (c/b)$$
which i suppose is right. However, in the intershield (a conductor) I realize that the field and therefore the potential difference must be zero:
$$\int_{intershield} \textbf{E} \cdot \textbf{S} = E(r) \pi 2 r L = (Q_1-Q_1) / \epsilon_0 = 0$$
I just cannot come to peace with the fact that there is a non-zero field inside the intershield. But I guess that the net charge rude man mentioned goes into charging the generator and thus supply static electricity for the bold physicist. I have tried to find info about the high voltage van de graaf generator on the internet and on physics forum without success. This is bad because I feel I have a major misconception connected to this.

 

[voko]

You could treat the system as if it was composed of two nested cylindrical capacitors, with four surfaces overall, A, B, C, D, counting from the center. There is field between A and B and between C and D, and B and C are connected and kept at the same potential. You could also say that they are infinitely close to each other.

 

[rude man]

I just cannot come to peace with the fact that there is a non-zero field inside the intershield. But I guess that the net charge rude man mentioned goes into charging the generator and thus supply static electricity for the bold physicist. I have tried to find info about the high voltage van de graaf generator on the internet and on physics forum without success. This is bad because I feel I have a major misconception connected to this.

Take a bit of metal and charge it, what do you get? You get charges on the surface of the metal. The field inside the metal is zero.

This is the case with the shield. There is no E field inside the shield. The charges are on the surfaces. -Q1 is on the inside surface and +Q2 is on the outside surface.

Your picture should show -Q1 onthe inside surface of the shield and +Q2 on the outside surface.

Integrating the field from one surface to the other is a tricky business. Essentially, the field is infinite right where the charges are, and zero inside. In the case of the shield, the E field changes from Q1/2πεLb r just outside the inside surface to Q2/2πεLb r just outside the outside surface, where r is the unit radial vector. You get infinite dE/dr as you pass thru the inside charge layer and then again as you pass thru the outside layer, and the result is ΔE = E2 - E1 = ∫(dE2/dr - dE1/dr)dr = (Q2 - Q1)/2πεLb.

 

[Order]

End of thread

You could treat the system as if it was composed of two nested cylindrical capacitors, with four surfaces overall, A, B, C, D, counting from the center. There is field between A and B and between C and D, and B and C are connected and kept at the same potential. You could also say that they are infinitely close to each other.

Ok, I Always thought that the intershield was a conductor or at least a dielectric (which is not covered in the chapter) but it is just a gas there and the intershield is just a cylindrical plate. (Why couldn't they say that, I was so confused.) Well that explains a lot. Thanks a bunch voko and rude man. I will probably be back with more questions!

 

[Order]

Take a bit of metal and charge it, what do you get? You get charges on the surface of the metal. The field inside the metal is zero.

This is the case with the shield. There is no E field inside the shield. The charges are on the surfaces. -Q1 is on the inside surface and +Q2 is on the outside surface.

Your picture should show -Q1 onthe inside surface of the shield and +Q2 on the outside surface.

Integrating the field from one surface to the other is a tricky business. Essentially, the field is infinite right where the charges are, and zero inside. In the case of the shield, the E field changes from Q1/2πεLb r just outside the inside surface to Q2/2πεLb r just outside the outside surface, where r is the unit radial vector. You get infinite dE/dr as you pass thru the inside charge layer and then again as you pass thru the outside layer, and the result is ΔE = E2 - E1 = ∫(dE2/dr - dE1/dr)dr = (Q2 - Q1)/2πεLb.

Yes there is that discontinuity of the field that i did not Count on. I guess I was just fooled by the Picture, or rather by myself Much ado about nothing then.

 

[rude man]

Yes there is that discontinuity of the field that i did not Count on. I guess I was just fooled by the Picture, or rather by myself Much ado about nothing then.

So did you ever solve for V1 and V2?

 

[Order]

So did you ever solve for V1 and V2?

Oh sure, I got the same result as voko already shared a few posts ago:
Between terminal and intershield
$$\Delta \phi_1 = \phi(a)-\phi(b)=E_{max}a\ln (b/a)=12.3 MV$$
Between intershield and outer shell
$$\Delta \phi_2 = \phi(b)-\phi(c)=E_{max}b\ln (c/b)=18.8 MV$$
And the total Voltage, if the Shell voltage is zero, then V₂=31.1 MV, and V₂= 18.8 MV, just as they should be.

 

[rude man]

Oh sure, I got the same result as voko already shared a few posts ago:
Between terminal and intershield
$$\Delta \phi_1 = \phi(a)-\phi(b)=E_{max}a\ln (b/a)=12.3 MV$$
Between intershield and outer shell
$$\Delta \phi_2 = \phi(b)-\phi(c)=E_{max}b\ln (c/b)=18.8 MV$$
And the total Voltage, if the Shell voltage is zero, then V₁=31.1 MV, and V₂= 18.8 MV, just as they should be.

Good! I hadn't noticed voko gave the potentials a while ago. Anyway, those agree with mine.