- #1
robertjford80
- 388
- 0
Homework Statement
I thought sometimes the integral of e^x is xe^x. Under what circumstances is the integral of e^x = xe^x? I think it has something to do with u substitution.
robertjford80 said:Homework Statement
I thought sometimes the integral of e^x is xe^x. Under what circumstances is the integral of e^x = xe^x? I think it has something to do with u substitution.
HallsofIvy said:The derivative of [itex]xe^x[/itex] is, by the product rule [itex](x)'e^x+ (x)(e^x)'= 1(e^x)+ x(e^x)= xe^x+ e^x= (x+ 1)e^x[/itex]. As Ray Vickson said, the integral of [itex]xe^x[/itex] is NOT equal to itself and neither is the derivative.
The only functions having the property that their derivative is equal to the function itself is a constant times [itex]e^x[/itex].
What's going on with the derivative of c1e(3/2)x[ is mainly the chain rule.robertjford80 said:Here's an example
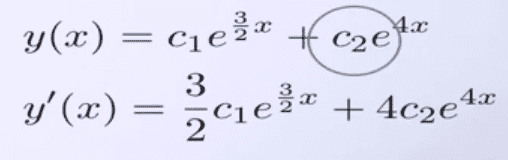
What's going on here? It clear says that the derivative of
c1e(3/2)x[ = (3/2)c1e(3/2)x
robertjford80 said:so the integral of e^2x is e^2x and the derivative of e^x is e^x but the derivative of e^2x is 2e^2x, is that right?
robertjford80 said:well, why don't you use the chain rule with e^x which would make it xe^x?
{this referred to number nine's deleted post} i saw it before he deleted it.
robertjford80 said:so the integral of e^2x is e^2x and the derivative of e^x is e^x but the derivative of e^2x is 2e^2x, is that right?
robertjford80 said:thanks villyer, I hadn't thought about that.
sharks said:The derivative of [itex]e^x[/itex] is: [tex]e^x .\frac{d(x)}{dx}[/tex]
robertjford80 said:if you're talking about post 4, then i don't think you provided enough info to convey that
It's obvious that [itex]\frac{dx}{dx}=1[/itex] which gives [itex]e^x .1=e^x[/itex]. Unless, you didn't know that, but it's really a basic notion of the principles of differentiation.sharks said:The derivative of [itex]e^x[/itex] is: [tex]e^x .\frac{d(x)}{dx}[/tex]
robertjford80 said:if it was obvious i would not have posted the question
The integral of e^x represents the area under the curve of the function e^x from a given starting point to a given ending point.
The formula for the integral of e^x is ∫e^x dx = e^x + C, where C is the constant of integration.
The integral of e^x is equal to xe^x when the lower limit is 0 and the upper limit is x.
The integral of e^x can be solved by using integration by parts or by using the substitution method.
The integral of e^x is important in mathematics and science because it is used to solve various problems involving exponential growth and decay, as well as in the calculation of probabilities and areas under curves in statistics and physics.