- #1
seiseilim
- 1
- 0
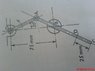
In the plane mechanism shown,the driving crank OA,which is 50mm between centers,oscillates about the fixed axis O.The rod ZC,which is uniform,100mm long and of tatol mass 0.05kg,slides through the trunnion(swiveling pin)B.The distance OB is 75mm.When the crank OA is at the position shown,it has an anticlockwise angular velocity of 40rad/s and zero angular acceleration.Assume that the masses of all moving links of other than rod AC and the effects of friction and gravity are to be neglected.For the position shown determine the reaction force between the rod AC and the trunnion B.
(this is my mid term question,but my lecturer nevr discuss about it.)
(this is my mid term question,but my lecturer nevr discuss about it.)