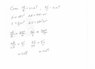Thermal Expansion of Spheres

[harshaxnim]

Explain why the thermal expansion of a spherical shell made of a homogeneous solid is equivalent to that of solid sphere of the same material.



I guess these equations would be of some help.
(ΔA)=A*2α*(ΔT)
α→ Coefficient of linear expansion.
A→ Area
T→ Temperature

(ΔV)=V*3α*(ΔT)
α→ Coefficient of linear expansion.
V→ Volume
T→ Temperature




I'm not sure if i understood the question right.
By "equivalent thermal expansion" i guess they mean to say the radius increases by same amount during the expansion.
So i set out relating the two radii.
Took two spheres, one hollow, the other solid, of same dimensions, i.e., same radii.



For the Shell,

(ΔA)=A*2α*(ΔT)
R_f²-R_i²=R_i²*2α*ΔT
R_f=R_i√(2α*ΔT+1)

For the solid sphere, similarly, relating the volume,
R_f=R_i∛(3α*ΔT+1)


But, failed to prove them to be the same.
So what exactly do they intend to ask? And how do i hit it?...

 

[Spinnor]

Does this work?