- #1
dalitwil
- 23
- 0
Ok guys, my last questions of the semester, Yay!
So I have two of them, one pertaining to a figure (attached), which has me terribly confused:
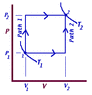
1.) In the figure (attached), if P1 = 133 kPa, V1 = 1123 cm3 and P2 = 200 kPa, V2 = 10000 cm3, what is the heat absorbed (+) or liberated (-), to the nearest joule, in Path 2? Assume the change in internal energy is 8900 J.
My Work (Reasoning):
I am assuming that W=0, simply because the path appears to be only vertical, So using ΔU=Q-W, we can say that ΔU=Q (because W=0) and ΔU is given as 8900 J, so wouldn't this be the answer? (It is not)
2.) 10 moles of a gas in thermal contact with an oil bath at temperature 300 K is compressed isothermally from a volume of 7541 cm3 to a volume of 1561 cm3. To the nearest joule what is the work done by the piston?
My Work:
W would simply equal nRT*ln(Vf/Vi)
Plugging in the knowns leaves me with -131
This is incorrect. (using the reasoning that ΔU=0)
Any ideas guys?
So I have two of them, one pertaining to a figure (attached), which has me terribly confused:
1.) In the figure (attached), if P1 = 133 kPa, V1 = 1123 cm3 and P2 = 200 kPa, V2 = 10000 cm3, what is the heat absorbed (+) or liberated (-), to the nearest joule, in Path 2? Assume the change in internal energy is 8900 J.
My Work (Reasoning):
I am assuming that W=0, simply because the path appears to be only vertical, So using ΔU=Q-W, we can say that ΔU=Q (because W=0) and ΔU is given as 8900 J, so wouldn't this be the answer? (It is not)
2.) 10 moles of a gas in thermal contact with an oil bath at temperature 300 K is compressed isothermally from a volume of 7541 cm3 to a volume of 1561 cm3. To the nearest joule what is the work done by the piston?
My Work:
W would simply equal nRT*ln(Vf/Vi)
Plugging in the knowns leaves me with -131
This is incorrect. (using the reasoning that ΔU=0)
Any ideas guys?