- #1
rbarngrover
- 8
- 0
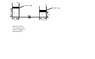
Two tanks filled with oil with density 860 kg/m3 are connected by a valve. Tank A has piston with 2.2 kg mass, cross sectional area of .02 m^3 and is suspended 1 m from the base of the tank. Tank B has a pistion mass of 1 kg, with cross sectional area .01 m^2 and is suspended .7m. when the valve is opened what are the final heights the two pistons are suspended.
I understand that Pressure of tank A has to equal Pressure tank B.
My main problem is i do not understand how i am suppose to correlate the two heights so i can solve for one of them. I tried have tank a height be x, then make tank b height be x-.3, but when u try and solve x cancels. Please would like to see how this is to go about being solved since most problems don't have the height's part of the problems.
I understand that Pressure of tank A has to equal Pressure tank B.
My main problem is i do not understand how i am suppose to correlate the two heights so i can solve for one of them. I tried have tank a height be x, then make tank b height be x-.3, but when u try and solve x cancels. Please would like to see how this is to go about being solved since most problems don't have the height's part of the problems.