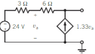
- #1
Frankenstein19
- 56
- 0
Homework Statement
[/B]
Homework Equations
The Attempt at a Solution
First I found the equivalent resistance since the 3 ohm resistor and 6 ohm resistor are in series. 9ohm. Then I did chose the node where the arrow points to as Voc, which is also va.
KVL:
(va+24V)/9ohm=1.33va
I get va to be 2.18
Then looking for Isc, I close the output terminals and then do kcl again on the node on top of the voltage controlled current source
1.33va-isc-24V/9ohm=0
and get isc=0.23
so Rt=2.18/0.23=9.47
The book says
isc=.24 and Rt=-3
I don't know what I'm doing wrong.