- #1
Tusike
- 139
- 0
Homework Statement
Hi! This problem was posted last month, and the due date was on the 10th so I can ask now.
Here is the problem: http://www.komal.hu/verseny/feladat.cgi?a=honap&h=201102&t=fiz&l=en"
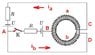
problem # P.4325
Homework Equations
Kirchoff's laws
The Attempt at a Solution
I know the magnetic flux can't change suddenly in time, which means that after closing the switch the total current inside the thoroid must remain I0. However, I have no idea how to calculate how much of this current goes through the "top" half of the toroid, and how much through the bottom. If I knew that I would be done, since the difference of the two is the current going through the switch. If anyone could start me off and guide me through this problem that'd be great and much appreciated.
Thanks!
-Tusike
Last edited by a moderator: