Tension in 3 Pulley System Homework

[Pi-Bond]

Homework Statement

(Kleppner & Kolenkow- An Introduction to Mechanics - 2.15)
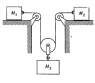
The image shows the setup. The task is to find the tension in the rope. The coefficient of friction of the sliding blocks with the surface is $\mu$, and the string is of constant length.

Homework Equations

Newton's Laws

The Attempt at a Solution

The question is easy enough if the accelerations of the three blocks can be related. I argued that when the lower block moves down a distance x₃, the pulley above it draws a string length equal to x₃. Since the length is constant, the string length drawn must equal the distance moved by the sliding blocks, i.e.

x₃=x₁+x₂

Differentiating twice with respect to time yields:

a₃=a₁+a₂

However this relationship yields the wrong answer. Any pointers on the correct relationship?

 

[Uncle_John]

Think again about your proposition that $x_{3} = x_{1} + x_{2}$. If you imagine for a moment that mass 1 is very big, it stands still, so only mass 2 moves. So if mass 2 moves for some distance l, how much does then mass 3 go up or down?

 

[cupid.callin]

John is right

and i solved the question ... I'm getting a pretty weird answer. Is the answer looong?

 

[gneill]

You can write expressions for the acceleration of each block from the FBD of each, assuming some unknown tension T in the rope. Call them a1, a2, a3 for the masses M1, M2, M3.

You can also divide the rope into two sections: L1 from M1 to M3, and L2 from M2 to M3. The sum of these two sections will be constant.

Assuming accelerations a1, a2, and a3, you can write expressions for the lengths of L1 and L2 with respect to time in terms of those accelerations. As stated previously, their sum must be constant for all time...

 

[gneill]

John is right

and i solved the question ... I'm getting a pretty weird answer. Is the answer looong?

What do you consider "looong"?

 

[cupid.callin]

maybe ... more than 4 things i numerator/denominator ... :grumpy:

ok you got me ... i can't define it ...

lets wait for the question to be solved ...

EDIT: smileys look good ... i might use them more often now ...

 

[ehild]

The Attempt at a Solution

I argued that when the lower block moves down a distance x₃, the pulley above it draws a string length equal to x₃.

Are you sure? Is not it twice x3?

ehild

 

[Pi-Bond]

Well I get the right answer when the sum of the sliding block's displacements is equal to twice the third block's displacement, but I can't reason why!

 

[gneill]

Well I get the right answer when the sum of the sliding block's displacements is equal to twice the third block's displacement, but I can't reason why!

Suppose for the sake of argument that the magnitude of the acceleration of M1 is a1, M2 is a2, and M3 is a3.

If the initial length of the rope segment from M1 to M3 is L1_o, what is an expression for the length of L1 as a function of time? Hint: it should depend only upon accelerations a1 and a3 and time.

 

[ehild]

Think: if you pull the lower block downward by x3, you pull the string at both sides of the pulley downward. So the hanging length of the string increases by 2x3, and this is equal to the sum of displacements of both sliding blocks.

ehild

 

[Modulated]

How much rope is "used up" to move a sliding block 1 cm?

How much rope is "used up" to move the falling block 1 cm?

 

[Pi-Bond]

Ah ok - I get it now! The string gets pulled down on both sides of the hanging pulley for a unit displacement, which leads to the relation: 2a₃=(a₁+a₂)

From application of Newton's second law to each mass, the relevant equations of this system are:

$m_{1}a_{1}=T-\mu m_{1}g$
$m_{2}a_{2}=T-\mu m_{2}g$
$m_{3}a_{3}=m_{3}g-2T$
$a_{3}=\frac{(a_{1}+a_{2})}{2}$

Simultaneous solution of these equations yields the correct value of Tension:

$T=\frac {g(\mu + 1)} {2m_{3}^{-1} + (2m_{1})^{-1} + (2m_{2})^{-1}}$

Thanks a lot everyone for the insight!

 

[gneill]

Can you justify your fourth equation? It seems odd (to me) that the acceleration of M3 should be twice the sum of the others...

 

[Pi-Bond]

Ah sorry, it's a typo! I meant it to be half!

 

[gneill]

Ah sorry, it's a typo! I meant it to be half!

Half looks better

 

[autodidude]

I'm currently working on this problem too and have run into the same problem but I can't understand why if the vertical displacement of M3 is twice the horizontal displacement of M1 and M2

If one side of the string is attached to a ceiling and we just move M1 (so I think the same as what the second post said) wouldn't moving M1 some distance equal the distance M3 is lowered?

 

[gneill]

If one side of the string is attached to a ceiling and we just move M1 (so I think the same as what the second post said) wouldn't moving M1 some distance equal the distance M3 is lowered?

Consider a pulley and rope with one end of the rope secured to the ceiling and the other end is lowered by a distance L. This amount of rope, L, must equal the total of the amount of rope gained on each side of the pulley as it falls. Thus L = L/2 + L/2, and the pulley moves down by half the amount that the rope end was moved. Note that this also accounts for the mechanical advantage inherent in this setup -- the load (pulley) moves half the distance that the input moves.

 

[autodidude]

Thanks gneill! Makes sense now!

 

[tms]

Delete.