- #1
Dimani4
- 50
- 0
Hi guys,
I have a question to all of you. This question is based on the example which is located here: http://galileo.phys.virginia.edu/classes/252/time_dil.html
I understand it but there is one thing is still unclear to me. So, here it is:
Again we have Jill on the rocket and poor Jack on the ground. So let's look at the picture 1. Jack synchronized his 2 clocks C1 and C2. Afterwards Jacks walks to the second clock C2 to meet Jill. When Jill passing clock C1 (with constant velocity) she synchronizes her clock with Jack's clock C1. After she passes 18*10^8m clock C2 should show 10sec then Jack sees on C2 10sec but when he looks at Jill's clock he sees 8sec (10sec*0.8). My question is what happens what Jill sees when she's looking at the Jack's clock? For her the train of 2 clocks (red frame) moving in the left direction (picture 2) with velocity of 1.8*10^8m/s. For her the distance that clock C2 should pass is (18*10^8m*0.8). So her clock is showing the same time (as for the case when Jack is looking at the Jill's clock) [18*10^8m*0.8/1.8*10^8m/s=10sec] but when she's looking at the Jack's clock she should see time less than 10sec because for her this time Jack's moving then his clock should be 8sec*0.8. But as I understand this is not right because she also should see the same 10sec. Again for Jack's frame of reference: Jack's clock shows 10sec, Jill's clock as Jack sees is 8sec. For Jill's frame of reference: Her clock shows 8sec but Jack's clock shows... (what?)
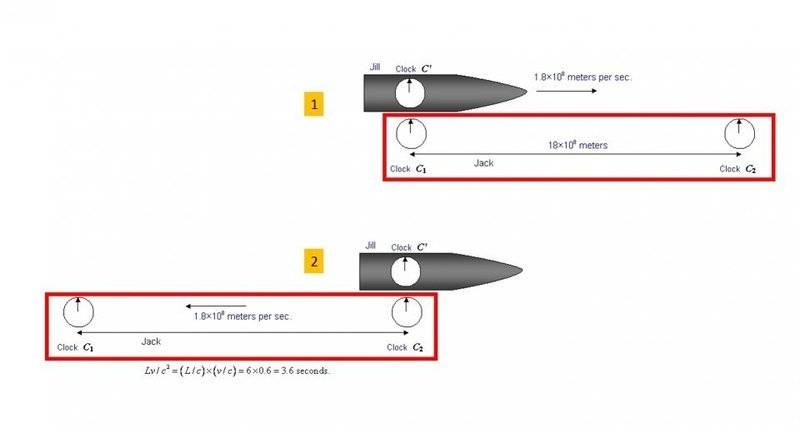 Picture2 shows the final state as Jill sees when the clocks (train of clocks) moved left.
Picture2 shows the final state as Jill sees when the clocks (train of clocks) moved left.
Thank you.
I have a question to all of you. This question is based on the example which is located here: http://galileo.phys.virginia.edu/classes/252/time_dil.html
I understand it but there is one thing is still unclear to me. So, here it is:
Again we have Jill on the rocket and poor Jack on the ground. So let's look at the picture 1. Jack synchronized his 2 clocks C1 and C2. Afterwards Jacks walks to the second clock C2 to meet Jill. When Jill passing clock C1 (with constant velocity) she synchronizes her clock with Jack's clock C1. After she passes 18*10^8m clock C2 should show 10sec then Jack sees on C2 10sec but when he looks at Jill's clock he sees 8sec (10sec*0.8). My question is what happens what Jill sees when she's looking at the Jack's clock? For her the train of 2 clocks (red frame) moving in the left direction (picture 2) with velocity of 1.8*10^8m/s. For her the distance that clock C2 should pass is (18*10^8m*0.8). So her clock is showing the same time (as for the case when Jack is looking at the Jill's clock) [18*10^8m*0.8/1.8*10^8m/s=10sec] but when she's looking at the Jack's clock she should see time less than 10sec because for her this time Jack's moving then his clock should be 8sec*0.8. But as I understand this is not right because she also should see the same 10sec. Again for Jack's frame of reference: Jack's clock shows 10sec, Jill's clock as Jack sees is 8sec. For Jill's frame of reference: Her clock shows 8sec but Jack's clock shows... (what?)
Thank you.