How Does the Period of a Spinning Disk Pendulum Change?

[Saitama]

Homework Statement

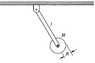
Find the period of a pendulum consisting of a disk on mass M and radius R fixed to the end of a rod of length l and mass m. How does the period change if the disk is mounted to the rod by a frictionless bearing so that it is perfectly free to spin?

Homework Equations

The Attempt at a Solution

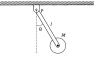
If the rod is displaced by an angle $\theta$ as shown in the attachment 2, the torque acting about the fixed point P is
$$\tau=-\frac{mgl}{2}\sin\theta-Mgl\sin\theta$$
From small angle approximation, $\sin\theta \approx \theta$. The moment of Inertia about P is
$$I=\frac{ml^2}{3}+M\left(\frac{R^2}{2}+l^2\right)$$
Let $\alpha$ be the angular acceleration, then
$$\alpha=-\frac{gl\theta}{I}\left(\frac{m}{2}+M\right)$$

Is this correct?

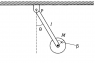
Moving to the second part of the question, I am thinking of assigning two angular velocities to the disk, $\omega_1=\dot{\theta}$ about P and $\omega_2=\dot{\beta}$ about CM of disk. Next I will write the expression for energy at any instant and differentiate it wrt time to find the time period. See attachment 3.

I came up with this: $R\beta=l\theta$. Is this correct? Is my approach correct?

Any help is appreciated. Thanks!

 

[arildno]

Remember that if you let the disk spin without friction at the axle, there are no torques that will affect that angular velocity.
Thus, you can regard w_2 as a constant.

 

[Saitama]

Remember that if you let the disk spin without friction at the axle, there are no torques that will affect that angular velocity.
Thus, you can regard w_2 as a constant.

So that means the time period won't change? Is my attempt at the first part correct?

I think my answer to the first part is correct. I checked it by letting m=0 and $R\rightarrow 0$. This gives the time period of simple pendulum.

 

[arildno]

Yes, I believe the first part is correct (don't remember the appropriate moments of inertia right now, but that's the only place it might be wrong.

For the second, let's look at the angular momentum about P for a spinning disk, positioned at distance R along the swinging rod.

A particular point on the disk has position vector:
$$\vec{p}=l\vec{i}_{L}+r\vec{i}_{R}$$
where, say, $\vec{i}_{L}=\sin\theta_{1}(t)\vec{i}-\cos\theta_{1}(t)\vec{j}$
while the radius vector in the Cartesian system fixed to the C.M of the disk can be written as:
$\vec{i}_{R}=\cos(\omega_{2}t)\vec{i}+\sin(\omega_{2}t)\vec{j}$
We then have, for the velocity of that point:
$$\vec{v}_{p}=l\omega_{1}(t)\vec{i}_{\theta_{1}}+r\omega_{2}\vec{i}_{theta_{2}}$$
setting the particle mass at $\delta{m}$, the contribution to the disk's angular momentum is:
$$\vec{p}\times{\delta{m}}\vec{v}_{p}=\delta{m}(l^{2}\omega_{1}(t)\vec{k}+ r^{2}\omega_{2}\vec{k}+lr\omega_{2}\vec{i}_{L}\times\vec{i}_{\theta_{2}}+lr\omega_{1}\vec{i}_{R}\times\vec{i}_{\theta_{1}})$$
The last two terms must be scrutinized some more..

We have (**):
$$\vec{i}_{L}\times\vec{i}_{\theta_{2}}=(\sin\theta_{1}(t)\vec{i}-\cos\theta_{1}(t)\vec{j})\times(-\sin\theta_{2}\vec{i}+\cos\theta_{2}\vec{j})=\sin(\theta_{1}-\theta_{2})\vec{k}$$
and similarly for the other.

Now, to sum up the net effect for the angular momentum for this term (**), we simply integrate over the full disk the angular momenta from all points, that is:
$$\int_{0}^{R}\int_{0}^{2\pi}lr\omega_{2}\sin(\theta_{1}-\theta_{2})\delta{m}$$
But, since we have $-\cos(\theta_{1}-0)=-\cos(\theta_{1}-2\pi)$
we see that these cross terms do NOT bring into the total angular momentum any effects at all!

That is, the spinning of the disk won't affect the period of the system, since we also have that w_2 will be a constant.

 

[arildno]

Okay, I overcomplicated it a bit.
You can, of course, use the energy equation and derive the same result; I showed how it directly follows from the primitive equation for the angular momentum.

 

[Saitama]

Okay, I overcomplicated it a bit.
You can, of course, use the energy equation and derive the same result; I showed how it directly follows from the primitive equation for the angular momentum.

Lets write down the energy equation for the first part of the question when the disk does not spin freely.
$$E=P.E + \frac{1}{2}I\omega^2$$
where P.E denotes the potential energy and I is the moment of inertia of system as calculated in #1.

For the case 2, when the disk spins about the axis passing through CM.
$$E=P.E + \frac{1}{2}I\omega^2 +\frac{1}{2}I'\omega'^2$$
where I' is the moment of inertia of disk about the axis through CM and $\omega'$ is the angular velocity about this axis. P.E is same in both the cases. Since the third term is constant as you say, differentiating any of the two expressions gives the same time period. So the time period does not change. Correct?

 

[arildno]

Yup!

 

[Saitama]

Yup!

Thanks a lot arildno! :)

 

[Enigman]

Lets write down the energy equation for the first part of the question when the disk does not spin freely.
$$E=P.E + \frac{1}{2}I\omega^2$$
where P.E denotes the potential energy and I is the moment of inertia of system as calculated in #1.

For the case 2, when the disk spins about the axis passing through CM.
$$E=P.E + \frac{1}{2}I\omega^2 +\frac{1}{2}I'\omega'^2$$
where I' is the moment of inertia of disk about the axis through CM and $\omega'$ is the angular velocity about this axis. P.E is same in both the cases. Since the third term is constant as you say, differentiating any of the two expressions gives the same time period. So the time period does not change. Correct?

I am not so sure, Pranav...
Here's what I think (I did this question a few days ago):
When you let the disc freely rotate it will no longer be a rigid body- the equation in #1 was for a rigid body( ie. $I=\frac{ml^2}{3}+M\left(\frac{R^2}{2}+l^2\right)$)
And moment of inertia won't be the same.
As,
$I_2=I_{rod\ about\ pivot}+I_{disc\ about\ pivot}$
$I_2=\frac{ml^2}{3}+Ml^2$($M\frac{R^2}{2}$won't contribute as its free to rotate about that axis)
And hence it should have a change in time period (according to me).

 

[arildno]

Enigman:
Ah, yes that is of course correct, and I forgot that this is, indeed, contained in my post on angular momentum in post 4. I completely forgot that the Mr^2/2 part in the first instance is locked to the angular velocity of the rod+disk system, while the corresponding part in the angular momentum equation in post 4 is MR^2/2w_2 (rather than MR^2/2w_1).

Since w_2 is constant, in contrast to w_1, there WILL be a change in the effective moment of inertia.
----
I apologize for having contributed to the confusion.

 

[arildno]

I made another mess-up in post 4 when I showed how we could use the primitive definition of angular momentum by computing the contributions from each material particle on the disk.
A material particle "p" has position, measured from point P:
$$\vec{p}_{p}=l\vec{i}_{L}+r\vec{i}_{r,p}, \theta_{2,p}(t)=\omega_{2}t+\theta_{0,p}$$
When we integrate over ALL material particles on the disk, we integrate for $0\leq{r}\leq{R},0\leq\theta_{0,p}\leq{2\pi}$

The results are unaffected, but apologies for my mess-up..

 

[Saitama]

I am not so sure, Pranav...
Here's what I think (I did this question a few days ago):
When you let the disc freely rotate it will no longer be a rigid body- the equation in #1 was for a rigid body( ie. $I=\frac{ml^2}{3}+M\left(\frac{R^2}{2}+l^2\right)$)
And moment of inertia won't be the same.
As,
$I_2=I_{rod\ about\ pivot}+I_{disc\ about\ pivot}$
$I_2=\frac{ml^2}{3}+Ml^2$($M\frac{R^2}{2}$won't contribute as its free to rotate about that axis)
And hence it should have a change in time period (according to me).

I don't get this. Why it doesn't contribute to the moment of inertia? "($M\frac{R^2}{2}$won't contribute as its free to rotate about that axis)", can you please elaborate this?

Thanks!

 

[arildno]

Pranav-Arora:
When the disk is FIXED, each material particle of the disk must share the angular velocity w_1, since they are part of the rigid body.
When the disk is NOT fixed, those material particles have angular velocity about its axis w_2, but that is a constant.

Thus, the rate of change of the ANGULAR MOMENTUM is different in the two cases
--------------------

 

[ehild]

There is no torque that would make the disk itself rotate with respect to the rest frame of reference. So the change of angular momentum comes from the rod with the disk as a point mass at its end.

ehild

 

[Saitama]

When the disk is NOT fixed, those material particles have angular velocity about its axis w_2, but that is a constant.

They have w_1 about the fixed point P too, no? I don't really see what I am missing here, I just can't understand the situation.

Enigman says that it will no longer be a rigid body. Why? Does it change the shape or is there something more to the definition of rigid body?

 

[arildno]

It is in the second instance, as ehild writes, ONLY as a point mass the disk contributes, not in addition to that as a disk.

 

[arildno]

They have w_1 about the fixed point P too, no? I don't really see what I am missing here, I just can't understand the situation.

Enigman says that it will no longer be a rigid body. Why? Does it change the shape or is there something more to the definition of rigid body?

1. "They have w_1 about the fixed point P too, no?"
THAT contribution will only be through being a concentrated point mass at L.
If you look at the point along the rod vector at distance L+R from P, then in your FIRST instance, the whole length L+R rotates with w_1, but in the second instance, the part to L (i.e, centre of mass of disk) rotates with w_1, but from L+R, w_2 is the local angular velocity followed.

2. "no longer be a rigid body. Why?"
Material points on the disk change, for example, their position relative to a fixed point on the rod. That is NOT true when the disk is firmly attached to it.

 

[arildno]

Remember:
For a RIGID body, ALL distances between material points on the body must remain constant throughout time. This is NOT the case when the disk allowed to rotate.

 

[Tanya Sharma]

If the disk is not fixed to the rod, then it will not rotate as the pendulum oscillates.Hence it does not contribute to the moment of inertia of the system. Please note that now the pendulum is no longer a rigid body as was the case when the disk was fixed.

So ,Moment of Inertia about pivot point =M I of the rod + M I of the disk treated like a point object.

 

[Saitama]

Remember:
For a RIGID body, ALL distances between material points on the body must remain constant throughout time. This is NOT the case when the disk allowed to rotate.

Ok, agreed. Is it possible to find w_2? Sorry if this is a dumb question.

 

[arildno]

Not a dumb question at all!
However:
Since w_2 is a CONSTANT, there is no dynamic equation within which it enters; at all times, it equals its initial value.

If, however, you nastify your problem by letting, say, a frictional force act about the axle through some constitutive law (say, proportional to the tangential velocity of your disk (which now is an annulus) about the axle), then you have 4 unknowns:
The two angular velocities and the horizontal and vertical constraint forces at P.

In that nasty scenario, you might use the two equations of motion Newton 2 yields, the angular momentum equation about P plus the condition that the velocity of the rod is 0 at P to gain your appropriate diff.eqs.

 

[Saitama]

Not a dumb question at all!
However:
Since w_2 is a CONSTANT, there is no dynamic equation within which it enters; at all times, it equals its initial value.

If, however, you nastify your problem by letting, say, a frictional force act about the axle through some constitutive law (say, proportional to the tangential velocity of your disk (which now is an annulus) about the axle), then you have 4 unknowns:
The two angular velocities and the horizontal and vertical constraint forces at P.

In that nasty scenario, you might use the two equations of motion Newton 2 yields, the angular momentum equation about P plus the condition that the velocity of the rod is 0 at P to gain your appropriate diff.eqs.

That's really complicated. I still need to understand your post #4. I will be spending time on it tonight. Anyways, thanks a lot for the help arildno, I should have been careful with the definitions.

And thank you Enigman! :)

 

[arildno]

Read the errata to post 4 as given in post 11.

To give you a lead:
the system's total angular momentum about P must be the sum (or integral) of all material particles' angular momenta about P.
In posts 4+11, I confine myself to the contribution to the total angular momentum, as given by the DISK-particle-subsystem; in addition to that, the contribution from the ROD-particle-subsystem must be added, in order to gain the WHOLE system's angular momentum.