- #1
Faradave
- 108
- 0
I'm a layman who’s spent a few weeks working through the FAQs and the two substantial sticky threads (most helpful, highly recommended). In order to avoid distraction, I have copied this post from its original location.
When we speak of “the universe”, it is important to acknowledge that we refer to all space (and its contents) at a given instant. (More specifically, we refer to all space for a set of comoving particles.) But the universe “now” applies to just one layer of space within spacetime. This occurs between adjacent layers for the immediate past and the immediate future.
Though the "reality" of it is disputable, it seems undeniable that, with respect to the balloon analogy (BA), time is radial. There is no other reasonable place for it in the model, we are not disavowing time, so it is completely within reason to ask where time belongs.
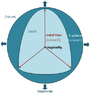
The whole purpose of the BA is to illustrate the expansion of space. In admitting this, we must concede that the balloon will be bigger at all future times and smaller at all past times. Space, collected for these times, forms concentric, onion-like layers. The next layer out is always larger than the one before it, demonstrating expansion with no obvious limit. Going the other way however, there is a limit, at the center of the onion, which I think we must also admit, is the region of the Big Bang event (a.k.a. Singularity). The universe (now) does not contain the Big Bang event but spacetime must.
My diagram is adapted from one on the net (not a science site.) The balloon surface is a 3-sphere, a flat representation of all three spatial dimensions. One might imagine a school globe but, instead of an ordinary map on its surface imagine a hologram. Even though its flat, it shows all three dimensions (latitude, longitude and altitude, in this case).
When we speak of “the universe”, it is important to acknowledge that we refer to all space (and its contents) at a given instant. (More specifically, we refer to all space for a set of comoving particles.) But the universe “now” applies to just one layer of space within spacetime. This occurs between adjacent layers for the immediate past and the immediate future.
Though the "reality" of it is disputable, it seems undeniable that, with respect to the balloon analogy (BA), time is radial. There is no other reasonable place for it in the model, we are not disavowing time, so it is completely within reason to ask where time belongs.
The whole purpose of the BA is to illustrate the expansion of space. In admitting this, we must concede that the balloon will be bigger at all future times and smaller at all past times. Space, collected for these times, forms concentric, onion-like layers. The next layer out is always larger than the one before it, demonstrating expansion with no obvious limit. Going the other way however, there is a limit, at the center of the onion, which I think we must also admit, is the region of the Big Bang event (a.k.a. Singularity). The universe (now) does not contain the Big Bang event but spacetime must.
My diagram is adapted from one on the net (not a science site.) The balloon surface is a 3-sphere, a flat representation of all three spatial dimensions. One might imagine a school globe but, instead of an ordinary map on its surface imagine a hologram. Even though its flat, it shows all three dimensions (latitude, longitude and altitude, in this case).
Attachments
Last edited:




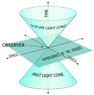




 I’m unable to expunge my prior HB references. Too bad no one said anything after my post #12 (
I’m unable to expunge my prior HB references. Too bad no one said anything after my post #12 (