Torque and the forces that affect it

[klandestine]

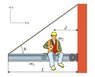
This problem is regarding the attached jpeg.

I am supposed to find the tension in the cable. I know that since the setup is in equilibrium, all net forces and torques equal zero. So,

Since net F(x) = 0, Tcos@ = F
and net F(y) = 0, Tsin@ = g(m1+m2)

@=theta
F=the normal force exerted by the wall

Also, the center of mass is (m1(L/2)+m2(d))/( m1+m2)

I know that the net torque is zero, otherwise the beam would be rotating. If I chose the cm as the point around which i calculate this torque, do I count the weight of the beam and the man? I want to say no, because if this is pointing straight down on the axis, it won't cause rotation. But I don't have a really good grasp of torque.

 

[whozum]

That would work but you have to realize the beam is a rigid object, and in torque problems, you'd have to take into account the mass distribution.

I would put my fulcrum to the left of the man, on the red bar.

From there Torque_down = mass_man*d + inertia_bar*L
Torque_up = Rope = Torque_down

 

[klandestine]

but that doesn't take into account gravity

 

[whozum]

Sorry its late.

Torque_down = Force_man*d + Force_bar*L
The up torque is still the same.

For the torque of the bar you'll need to find the moment of inertia of a bar which I think is mR^2/12

 

[Doc Al]

I know that the net torque is zero, otherwise the beam would be rotating. If I chose the cm as the point around which i calculate this torque, do I count the weight of the beam and the man? I want to say no, because if this is pointing straight down on the axis, it won't cause rotation.

Exactly correct! If you calculate torque about the cm, you can ignore the weight of the man + beam. Unfortunately, however, you would then have to include the torque contributed by the force exerted on the beam by the wall.

Much better is to choose the contact point with the wall as your pivot point in calculating torque. (Then you can ignore those wall forces since they act at the pivot point and contribute no torque about that point.) Add up the torques (due to the tension and the weights of the man and beam) about that point and set the sum equal to zero. Then you can solve for the only unknown, the tension.

 

[klandestine]

Thank you, Doc Al.

Would it be appropriate to extend your advice a general "rule":

If a force passes through a particular point in a system, then it will not exert a torque on that point.

Also, could you tell me how to enter mathematical symbols when posting - I couldn't really glean anything from the FAQ.

Thank you so much for your help.

 

[klandestine]

...and another...

The third part of this question asks me to find the y-component of force that the wall exerts on the beam (F), using the axis shown. I don't understand how the nomal force of the wall could have a y-component, since according to my free body diagram, it is simply a strictly horizontal force pointing left.

 

[whozum]

Friction between the wall and the bar is what keeps the bar up. The direction of this force is completely in the positive y direction.

start using [tex] [tex] [/tex]
make sure you close the tex tag with [/tex]
Then just type your equations out regularly

\frac{numerator}{denominator} = $$\frac{numerator}{denominator}$$
\int{integrand}{variable} = $$\int{integrand}{variable}$$
\theta, \omega, \pi, \epsilon , etc = $$\theta, \omega, \pi, \epsilon , etc$$

 

[Doc Al]

Would it be appropriate to extend your advice a general "rule":

If a force passes through a particular point in a system, then it will not exert a torque on that point.

Absolutely!

Also, could you tell me how to enter mathematical symbols when posting - I couldn't really glean anything from the FAQ.

The best way to learn is to copy others. Try poking around in this thread: https://www.physicsforums.com/showthread.php?t=8997; that's the place to learn and practice writing equations.

 

[Doc Al]

The third part of this question asks me to find the y-component of force that the wall exerts on the beam (F), using the axis shown. I don't understand how the nomal force of the wall could have a y-component, since according to my free body diagram, it is simply a strictly horizontal force pointing left.

Realize that the beam is attached to the wall, not just leaning against it. That connection allows the wall to exert a force in any needed direction. Just refer to that force by its components: $F_x$ & $F_y$.

If, instead, the beam were just leaning against the wall, you would need to consider both the normal force (horizontal) and any friction force (vertical). But that's not the case in this problem.

 

[klandestine]

Realize that the beam is attached to the wall, not just leaning against it. That connection allows the wall to exert a force in any needed direction. Just refer to that force by its components: $F_x$ & $F_y$.

Do you literally mean any direction?

And, would this 'transformable' force concept be applicable to non-rotational dynamics problems? For example, when I am writing the net forces in the x and y directions, do I include the force ofthe wall? Or, is this force only associated with torque?

 

[Doc Al]

Do you literally mean any direction?

Sure. The wall can push or pull, as needed, in any direction.

And, would this 'transformable' force concept be applicable to non-rotational dynamics problems? For example, when I am writing the net forces in the x and y directions, do I include the force ofthe wall? Or, is this force only associated with torque?

If you are analyzing the beam, then you'd better include all the forces acting on the beam: that certainly includes the force that the wall exerts on the beam! The wall force will definitely contribute to the net force on the beam. And, depending on where you choose your axis, it may also contribute to the net torque about that axis.

 

[klandestine]

Yes, that makes perfect sense.

So, the wall can push or pull in whatever direction it is needed. But, who is to say which direction it is needed? Could I say that the wall exerts whatever force is needed to make the torque zero?

I really appreciate your help, I have a much better understanding of rotational dynamics and torques now.

 

[Doc Al]

So, the wall can push or pull in whatever direction it is needed. But, who is to say which direction it is needed? Could I say that the wall exerts whatever force is needed to make the torque zero?

The force that the wall exerts on the beam is an example of a so-called passive force. Passive forces adjust themselves in response to "active" forces. Another example of a passive force is the tension in the cable. Pull on the cable as hard as you want (an active force) and the cable tension will adjust itself accordingly (a passive force). (There are limits, of course. Pull too hard and the cable will snap or yank itself out of the wall.)

I really appreciate your help, I have a much better understanding of rotational dynamics and torques now.

It is my pleasure. Qui docet discit. (He who teaches learns.)