- #1
thshen34
- 13
- 0
Homework Statement
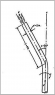
Consider a steady flow of liquid with a density of 805 kg/m3 through a rotating tube as shown in the sketch. The flow speed is V = 5 m/s. If ω = 10 rad/s, find the torque necessary to rotate the pipe. Assume a uniform velocity distribution at the exit from the pipe, and that the
incoming fluid has no angular momentum.
Homework Equations
I'm assuming we're using conservation of mass and/or conservation of angular momentum.
The Attempt at a Solution
I'd know what to do if the ω was in the plan of the paper, but it seems to be asking the torque to rotate the pipe about the sketched axis. However, the fluid forces from the fluid force points down and to the right, none of which create a moment about that axis, so there's no angular momentum. My other idea is that one of the components of the fluid's force is the centripetal force, which contributes to the ω. Does anyone else have any ideas regarding this problem?