- #1
amainejr
- 3
- 0
This problem should be an introductory physics problem, but I am not sure if I am going about it the right way. This Link is the total system that has been created, and I have attached an isolated image to clarify what I am about to ask, so please refer to that.
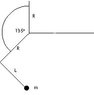
I have a point-mass (m) attached to a two arm system, noted as L and R. The upper arm is attached to a servo that has a range of 135 deg (0 deg is straight up in this instance). I know that the max torque on the upper arm will be when it is fully extended to the horizontal. I am drawing 2 free body diagrams for each arm, for maximum torque, where the lower arm is fixed (but free to rotate) about the upper arm. The lower arm will never reach an angle of more than 90 deg relative to the upper arm.
The problem I am running into, is that this isolated system is replicated 3 times, all supporting the mass m. Do I divide the mass by 3 for each system or is this problem much harder than that?
I have a point-mass (m) attached to a two arm system, noted as L and R. The upper arm is attached to a servo that has a range of 135 deg (0 deg is straight up in this instance). I know that the max torque on the upper arm will be when it is fully extended to the horizontal. I am drawing 2 free body diagrams for each arm, for maximum torque, where the lower arm is fixed (but free to rotate) about the upper arm. The lower arm will never reach an angle of more than 90 deg relative to the upper arm.
The problem I am running into, is that this isolated system is replicated 3 times, all supporting the mass m. Do I divide the mass by 3 for each system or is this problem much harder than that?