Torus Centre of Mass Question

[unscientific]

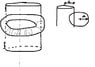
Homework Statement

The question is attached in the picture. I did part (a) without much problems.. But I have no clue what part (b) is about at all! Even the solutions don't make much sense to me.

The Attempt at a Solution

I tried to work out how the diagram would look like, illustrated in the second attachment. But still, I am lost...

 

[gabbagabbahey]

Look at a circular cross-section of the torus; since the cylinder is radius $c$, the same as the distance of the centre of the circular cross-section from the axis of the cylinder, the wall of the cylinder will divide the circular cross-section of the torus right down the middle. The surface area of the torus on either side of the divider will not be equal though, because one half is closer to the axis than the other half (Think of rotating a point around the axis, it scribes a cricle of circumference $2\pi r$ where $r$ is the distance from the axis)

 

[unscientific]

Look at a circular cross-section of the torus; since the cylinder is radius $c$, the same as the distance of the centre of the circular cross-section from the axis of the cylinder, the wall of the cylinder will divide the circular cross-section of the torus right down the middle. The surface area of the torus on either side of the divider will not be equal though, because one half is closer to the axis than the other half (Think of rotating a point around the axis, it scribes a cricle of circumference $2\pi r$ where $r$ is the distance from the axis)

I see! I've worked it out finally. Thanks! I wasn't sure what they meant by "cross section of radius a centred on a circle of radius c "..

Thanks for clearing it up!