Calculating Force of n Particles in R-l Container

[MMD]

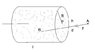
A container with radius R and height l contains n particles. If all particles in the container are equally distanced from each others by a distance and the force from each particles to the point A is f = K/ d^2 (K=constant and AB = d), please find the total force from all particles to the point A using integration (h = constant).

Please view the attachment for a figure illustrating the problem.

Thank you.

 

[cristo]

Do you have any thoughts on the question? Please note that we must see some work before we can help.

 

[m2003]

I would approach this problem by first understanding the physical principles involved. The given information suggests that the particles in the container are exerting a force on a specific point, A, within the container. This force is dependent on the distance between each particle and the point A, and is inversely proportional to the square of that distance. This is known as the inverse square law, and is a fundamental principle in physics.

To calculate the total force from all particles to point A, we can use the concept of integration. Integration is a mathematical tool that allows us to find the total value of a function over a certain range. In this case, we can integrate the force function (f = K/d^2) over the range of distances between the particles and point A, which is given as h.

To do this, we first need to express the force function in terms of the distance between each particle and point A. We can do this by using the Pythagorean theorem, which states that the distance between two points in three-dimensional space is the square root of the sum of the squares of the differences in each coordinate. In this case, the coordinates are the x, y, and z positions of each particle and point A.

Once we have the force function expressed in terms of the distance, we can then integrate it over the range of distances from 0 to h. This will give us the total force from all particles to point A.

It is important to note that the integration process will involve using the constant K, as well as the radius R and height l of the container. These parameters will play a crucial role in determining the final value of the force.

In conclusion, by using the concept of integration and the principles of physics, we can determine the total force from all particles to point A in the given container. This approach allows us to solve complex problems in a systematic and rigorous manner, making it an essential tool for any scientist.