- #1
Jake
- 90
- 0
This is a tough angle problem (For me),
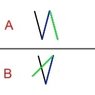
In the diagram below, I have two cases, A and B. In each case, when I sequentially compare the black, blue, and then green lines to the previous line, in each case you end up with the following angles: ~30 and ~30. Yet clearly the spatial relationships of the lines in cases A and B are different!
So how could I measure lines sequentially, so I can build up a relationship of 360 degree angles between the lines?
refering to the image, case A would rightfully measure ~30 degrees then ~330 degrees. case B would measure ~30 and ~30 again.
Hope that made sense.
Thanks!
In the diagram below, I have two cases, A and B. In each case, when I sequentially compare the black, blue, and then green lines to the previous line, in each case you end up with the following angles: ~30 and ~30. Yet clearly the spatial relationships of the lines in cases A and B are different!
So how could I measure lines sequentially, so I can build up a relationship of 360 degree angles between the lines?
refering to the image, case A would rightfully measure ~30 degrees then ~330 degrees. case B would measure ~30 and ~30 again.
Hope that made sense.
Thanks!
Attachments
Last edited: