- #1
Somefantastik
- 230
- 0
Hello,
I have a Jacobian matrix
[tex] A = \left( \begin{array}{cc}
-2x+1-a_{1}y & -a_{1}x \\
-a_{2}ry & r-2ry-ra_{2}x \end{array} \right)\ [/tex]
where
[tex] a_{1} > 1 \ ; \ a_{2} > 1 \ ; \ and \ r>0 [/tex]
the trace is
[tex]Tr(A) = 1-2x-a_{1}y+r(1-y-a_{2}x)-ry = x(-2-ra_{2}) +y(-a_{1}-2r)+1+r [/tex];
and the determinant is
[tex]det(A) = r(1-2y-a_{2}x-2x+4yx+2a_{2}x^{2}-a_{1}y+2y^{2}a_{1}) [/tex];
I need to show that Tr(A)>0 or det(A)<0. Neither one of them seem to be working out for me. Can anyone point me in the right direction? The point of this exercise is showing an equilibrium point is unstable.
Update: I can see from MATLAB that the determinant must be zero as the phase portrait shows a saddle point.
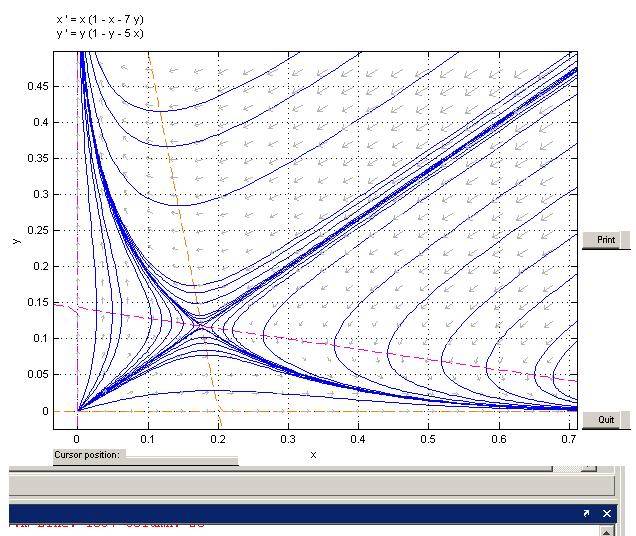
Please help me show det(A) < 0.
I have a Jacobian matrix
[tex] A = \left( \begin{array}{cc}
-2x+1-a_{1}y & -a_{1}x \\
-a_{2}ry & r-2ry-ra_{2}x \end{array} \right)\ [/tex]
where
[tex] a_{1} > 1 \ ; \ a_{2} > 1 \ ; \ and \ r>0 [/tex]
the trace is
[tex]Tr(A) = 1-2x-a_{1}y+r(1-y-a_{2}x)-ry = x(-2-ra_{2}) +y(-a_{1}-2r)+1+r [/tex];
and the determinant is
[tex]det(A) = r(1-2y-a_{2}x-2x+4yx+2a_{2}x^{2}-a_{1}y+2y^{2}a_{1}) [/tex];
I need to show that Tr(A)>0 or det(A)<0. Neither one of them seem to be working out for me. Can anyone point me in the right direction? The point of this exercise is showing an equilibrium point is unstable.
Update: I can see from MATLAB that the determinant must be zero as the phase portrait shows a saddle point.
Please help me show det(A) < 0.
Last edited: