- #1
AdityaDev
- 527
- 33
Homework Statement
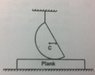
Lower surface of a plank is rough and is initially at rest on a horizontal floor. It's upper surface is smooth and has a smooth hemisphere place over it through a light string as shown. Find the trajectory of centre of mass of the sphere after the string is burnt.
Homework Equations
Nothing special here.
I think the question is testing some concept.
$$y_{cm}=R/2$$
X cm is zero.
{for hemisphere}
The Attempt at a Solution
Since the hemisphere is smooth,the velocity of the centre of the flat surface will be zero and its centre of mass will rotate about that point.(wrt plank).
Here since centre of mass of the system changes.so the plank will also move.
But there is friction between the plank and surface. Can you help me find its trajectory?