- #1
Styx
- 27
- 0
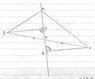
In the diagram, AM is a medium of triangle ABC. Perpendicular lines drawn from B and C to AM (or its extension) meet AM at P and Q respectively.
Prove that BP = CQ
So far I have concluded that:
BM = CM
Angle BPM = angle CQM
Triangle ABM = ACM
I am not sure what else I can do in order to prove that the triangles BMP and CMQ are congruent which would prove that BP = CQ
Prove that BP = CQ
So far I have concluded that:
BM = CM
Angle BPM = angle CQM
Triangle ABM = ACM
I am not sure what else I can do in order to prove that the triangles BMP and CMQ are congruent which would prove that BP = CQ
Attachments
Last edited: