- #1
DaTario
- 1,039
- 35
Hi All,
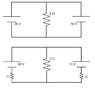
Concerning the first circuit in the attached figure:
By applying Kirchhoff laws we arrive at two different currents in the central resistor. But if we consider the second circuit with its auxiliar resistances we see no problem with the definition of the central current.
Is it due to the fact that batteries always have some resistance?
Infinite currents will appear in the side branches of this first circuit, but even so is there any way to get the appropriate answer to the question of what is the current in the central resistor?
I am not sure I have understood well the superposition principle which may well be the method to be used here (in the first circuit).
Thanks,
Best Wishes,
DaTario
Concerning the first circuit in the attached figure:
By applying Kirchhoff laws we arrive at two different currents in the central resistor. But if we consider the second circuit with its auxiliar resistances we see no problem with the definition of the central current.
Is it due to the fact that batteries always have some resistance?
Infinite currents will appear in the side branches of this first circuit, but even so is there any way to get the appropriate answer to the question of what is the current in the central resistor?
I am not sure I have understood well the superposition principle which may well be the method to be used here (in the first circuit).
Thanks,
Best Wishes,
DaTario