- #1
savva
- 39
- 0
Homework Statement
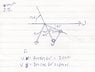
Resolve the force F1 into components acting along u and v axes and determine the magnitudes of the components. Refer to first attachment for full problem with diagram.
Homework Equations
asinθ
bcosθ
The Attempt at a Solution
Please refer to attachments for attempt at solution, drawings of diagram involved. Could not get the correct answer solving the way in which I attempted, can anybody give me a hand solving it, answers in the book were:
f1u=205N, f2v=160N