- #1
fishspawned
- 66
- 16
Homework Statement
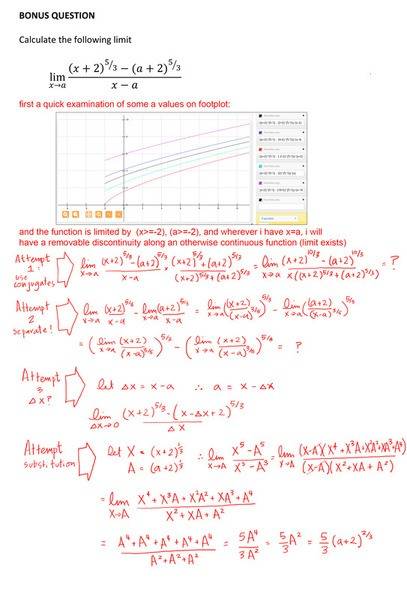
the limit x->a of [(x+2)^5/3 - (a+2)^5/3] / (x-a)
Homework Equations
limit laws
Correct result.fishspawned said:DELTA:
this seems to take care of it - provided you know how to expand a sum of powers to a high level - had to look it up to be honest:
so revised sheet:
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a particular value. It represents the value that a function approaches, but may never actually reach, as the input gets closer and closer to a specific value.
To find the limit of a function as its input approaches a particular value, you can use algebraic techniques, such as factoring or simplifying, or you can use graphical techniques, such as using a graphing calculator or graphing the function by hand. You can also use numerical methods, such as plugging in values close to the limit or using a calculator to calculate the function at different values.
A limit exists when the value that the function approaches as its input gets closer and closer to a particular value is equal to a single, finite value. This means that the function is well-defined and has a consistent value at that point, even if it is not defined at that exact point.
A left-sided limit is the value that the function approaches as its input gets closer and closer to a particular value from the left-hand side. Similarly, a right-sided limit is the value that the function approaches from the right-hand side. In some cases, these two limits may be different, indicating that the function has a discontinuity at that point.
Finding limits is important in calculus because it allows us to analyze the behavior of a function and make predictions about its values. Limits are also used to define other important concepts, such as derivatives and integrals, which are essential in various fields of science, engineering, and economics.