- #1
Kaldanis
- 106
- 0
I'm in the process of studying for my final and I just can't solve this problem:
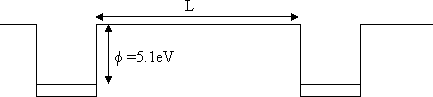
The work function (energy needed to remove an electron) of gold is 5.1 eV. Two pieces of gold (at the same potential) are separated by a distance L.
For what value of L will the transmission probability for an electron to cross from one to the other be T ≈ 10-3? Assume that G = 1 in the formula for the tunneling probability.
(a) L = 0.001 nm
(b) L = 0.02 nm
(c) L = 0.1 nm
(d) L = 0.3 nm
(e) L = 4
The attempt at a solution
I'm pretty sure I rearrange the tunneling equation and solve for L. Things are made easier since I'm told G=1. This means that [itex]L = -\frac{ln(T)}{2K}[/itex] , where [itex]K=\sqrt{\frac{2m}{\hbar}(U_{0-E})}[/itex]. My only problem is which values do I use for U0 and E?
The work function (energy needed to remove an electron) of gold is 5.1 eV. Two pieces of gold (at the same potential) are separated by a distance L.
For what value of L will the transmission probability for an electron to cross from one to the other be T ≈ 10-3? Assume that G = 1 in the formula for the tunneling probability.
(a) L = 0.001 nm
(b) L = 0.02 nm
(c) L = 0.1 nm
(d) L = 0.3 nm
(e) L = 4
The attempt at a solution
I'm pretty sure I rearrange the tunneling equation and solve for L. Things are made easier since I'm told G=1. This means that [itex]L = -\frac{ln(T)}{2K}[/itex] , where [itex]K=\sqrt{\frac{2m}{\hbar}(U_{0-E})}[/itex]. My only problem is which values do I use for U0 and E?