Two Charged Particles in SHM

[erok81]

Homework Statement

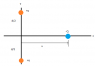
Two identical particles, each having charge +q, are fixed in space and separated by a distance d. A third particle with charge -Q is free to move and lies initially at rest on the perpendicular bisector of the two fixed charges a distance x from the midpoint between the two fixed charges. See image.

a) Show that if x is small compared with d, the motion of -Q is simple harmonic along the perpendicular bisector. Determine the period of that motion.

T=?

b) How fast will the charge -Q be moving when it is at the midpoint between the two fixed charges if initially it is released at a distance a<<d from the midpoint?

v_max=?

Homework Equations

I know Coulomb's Law and Hooke's law might be used somehow, but that's about where I am.

The Attempt at a Solution

I really don't even know where to start.

 

[rock.freak667]

What is the force between each of the +q charges and the -Q charge?

Shouldn't the horizontal component of this force be the resultant force?

For something to move with SHM a = -ω²x (so use Newton's 2^nd Law)

 

[erok81]

Your first two sentences I can see how to do. I just don't get how to relate F_e to SHM.

 

[rock.freak667]

Your first two sentences I can see how to do. I just don't get how to relate F_e to SHM.

Find the resultant force and put it equal to ma

 

[erok81]

I think I've forgotten a bit too much from Physics I.

I have no clue how to get from Newton's Law to period. I see you posted a = -ω2x, but I don't have an option to use omega. I only have k_e, q, Q, m, d, and a.

 

[rock.freak667]

I think I've forgotten a bit too much from Physics I.

I have no clue how to get from Newton's Law to period. I see you posted a = -ω2x, but I don't have an option to use omega. I only have k_e, q, Q, m, d, and a.

Forget about for now.

What is the horizontal resultant force? (first 2 lines of the second post)

 

[erok81]

Ok..turns out I can't solve that either. I am working from some pos e-book which is impossible to use.

I thought you had to break them down into components, but my book doesn't do that. Looking at an example in the book I get...

$$F_e=(k_e|q||-Q|)/x^2$$

I am assuming that the vertical components cancel leaving only the horizontal component.

 

[rock.freak667]

Ok..turns out I can't solve that either. I am working from some pos e-book which is impossible to use.

I thought you had to break them down into components, but my book doesn't do that. Looking at an example in the book I get...

$$F_e=(k_e|q||-Q|)/x^2$$

I am assuming that the vertical components cancel leaving only the horizontal component.

The force between two charges Q1 and Q2 separated by a distance r is

F= kQ₁Q₂/r²

What is the distance from -Q to either +q charges?

Hence what is the force between each pair of charges?

 

[erok81]

Ah...the distance would be √(x^2+(d^2/4))?

 

[rock.freak667]

Ah...the distance would be √(x^2+(d^2/4))?

Right, so then the force between +q and -Q at the top is? (This is the same as the force between -Q and +q at the bottom)

 

[erok81]

k|q||Q|/(√(x^2+(d^2/4))?

 

[rock.freak667]

k|q||Q|/(√(x^2+(d^2/4))?

Right, so then what is the horizontal component of this force?

 

[bubthegreat]

Working on the same problem here:
Wouldnt it be [(k|q||-Q|)/(d^2/4 + x^2)]cos(theta)? (then multiplied by 2 since the top and bottom combine?)
That's as far as I got on my own as well. Do we have to use the conservation of energy theorems and use that to find the angular velocity? ( If so, please remind me of the equation!)

 

[rock.freak667]

Working on the same problem here:
Wouldnt it be [(k|q||-Q|)/(d^2/4 + x^2)]cos(theta)? (then multiplied by 2 since the top and bottom combine?)

Yes. Also you can remove the | | signs and just write it as

$$F = \frac{-2kQq}{\frac{d^2}{4}+x^2}cos \theta$$

That's as far as I got on my own as well. Do we have to use the conservation of energy theorems and use that to find the angular velocity? ( If so, please remind me of the equation!)

You can forget about finding the ω for the moment.

Now that you have the component, looking at the triangle formed, can you use basic trigonometry to write cosθ in terms of d and x ?

 

[bubthegreat]

Cos(theta)=sqrt(d^2/4+x^2)/x if I'm understanding what you're asking for correctly. Am I? :P Would you mind explaining what you're walking me through? I know you're going somewhere with this, so I'm curious, and obviously need to understand if I'm going to get it right, hehe.

btw, here's the picture of the problem we're asked to do.

http://www.webassign.net/pse/p23-12.gif

thanks for the help

 

[rock.freak667]

Would you mind explaining what you're walking me through? I know you're going somewhere with this, so I'm curious, and obviously need to understand if I'm going to get it right.

Well we are trying to show that it moves with SHM right? To do that, one usually finds the resultant force and then applies Newton's 2^nd law. Thus far we are finding the resultant force.

Cos(theta)=sqrt(d^2/4+x^2)/x if I'm understanding what you're asking for correctly. Am I? :P

I think you inverted it, it should be cosθ = x/√(d²/4+x²)

So now we have this

$$F = \frac{-2kQq}{\frac{d^2}{4}+x^2} \frac{x}{\sqrt{\frac{d^2}{4}+x^2}}$$

Looks a bit complicated but that's ok. They say that x is small, so what does that mean for x² or any other higher powers of x? (say x = 0.0001, x² is smaller, x³ will be even smaller,etc.)